Second Scientific Lecture-Course:
Warmth Course
GA 321
2 March 1920, Stuttgart
Lecture II
My dear friends,
[ 1 ] Yesterday I touched upon the fact that bodies under the influence of heat expand. Today we will first consider how bodies, the solid bodies as we call them, expand when acted upon by the being of warmth. In order to impress these things upon our minds so that we can use them properly in pedagogy—and at this stage the matter is quite simple and elementary—we have set up this apparatus with an iron bar. We will heat the iron bar and make its expansion visible by noting the movements of this lever-arm over a scale. When I press here with my finger, the pointer moves upwards. (see drawing.)
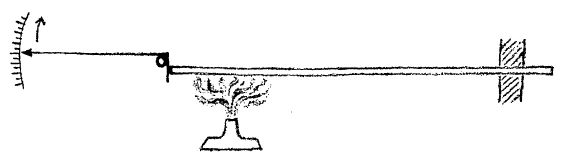
[ 2 ] You can see when we heat the rod, the pointer does move upwards which indicates for you the act that the rod expands. The pointer moves upwards at once. Also you notice that with continued heating the pointer moves more and more, showing that the expansion increases with the temperature. If instead of this rod I had another consisting of a different metal, and if we measured precisely the amount of the expansion, it would be found other than it is here. We would find that different substances expanded various amounts. Thus we would be able to establish at once that the expansion, the degree of elongation, depended on the substance. At this point we will leave out of account the fact that we are dealing with a cylinder and assume that we have a body of a certain length without breadth or thickness and turn our attention to the expansion in one direction only. To make the matter clear we may consider it as follows:
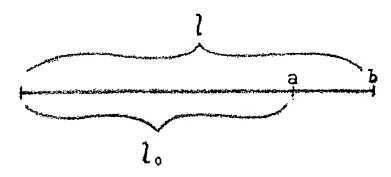
Here is a rod, considered simply \(l_o\) the length of the rod at the original temperature, the starting temperature. The length attained by the rod when it is heated to a temperature \(y\), we will indicate by \(l\). Now I said that the rod expanded to various degrees depending upon the substance of which it is composed. We can express the amount of expansion to the original length of the rod. Let us denote this relative expansion by \(\alpha\). Then we know the length of the rod after expansion. For the length \(l\) after expansion may be considered as made up of the original length \(l_o\) and the small addition to this length contributed by the expansion. This must be added on. Since I have denoted by \(\alpha\) the fraction giving the ratio of the expansion and the original length, I get the expansion for a given substance by multiplying \(l_o\) by \(\alpha\). Also since the expansion is greater the higher the temperature, I have to multiply by the temperature \(t\). Thus I can say the length of the rod after expansion is:
\(l = l_o + l_o \alpha t\), which may be written \(l_o (1 + \alpha t)\).
[ 4 ] Stated in words: if I wish to determine the length of a rod expanded by heat, I must multiply the original length by a factor consisting of \(1\) plus the temperature times the relative expansion of the substance under consideration. Physicists have called \(\alpha\) the expansion coefficient of the substance considered.
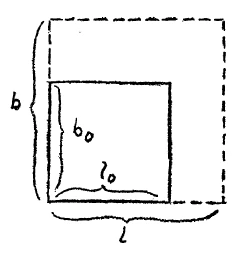
[ 5 ] Now I have considered here a rod. Rods without breadth and thickness do not exist in reality. In reality bodies have three dimensions. If we proceed from the longitudinal expansion to the expansion of an assumed surface, the formula may be changed as follows: let us assume now that we are to observe the expansion of a surface instead of simply an expansion in one dimension. There is a surface. This surface extends in two directions, and after warming both will have increased in extent. We have therefore not only the longitudinal expansion to \(l\) but also an increase in the breadth to \(b\) to consider. Taking first the original length, \(l_o\), we have as before the expansion in this direction to \(l\) or
$$l = l_o (1 + \alpha t) \qquad (1)$$[ 6 ] Considering now the breadth \(b_o\) which expands to \(b\), I must write down:
$$b=b_o(1+ \alpha t) \qquad (2)$$
[ 7 ] (It is obvious that the same rule will hold here as in the case of the length.) Now you know that the area of the surface is obtained by multiplying the length by the breadth. The original area I get by multiplying \(b_o\) and \(l_o\), and after expansion by multiplying \(l_o (1 + \alpha t)\) and \(b_o (1 + \alpha t)\)
$$lb=l_o (1 + \alpha t)b_o(1 + \alpha t) \qquad (3)$$
or
$$lb = l_o b_o (1 + \alpha t)^2 \qquad (4)$$or
$$Lb = l_o b_o (1 + 2 \alpha t + \alpha^2 t^2) \qquad (5)$$[ 8 ] This gives the formula for the expansion of the surface. [ 9 ] If now, you imagine thickness added to the surface, this thickness must be treated in the same manner and I can then write:
$$lbd = l_ob_od_o(1 + 3 \alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3) \qquad (6)$$[ 10 ] When you look at this formula I will ask you please to note the following: in the first two terms of you see \(t\) raised no higher than the first power; in the third term you see the second, and in the fourth term it is raised to the third power. Note especially these last two terms of the formula for expansion. Observe that when we deal with the expansion of a three-dimensional body we obtain a formula containing the third power of the temperature. It is extremely important to keep in mind this fact that we come here upon the third power of the temperature.
[ 11 ] Now I must always remember that we are here in the Waldorf School and everything must be presented in its relation to pedagogy. Therefore I will call your attention to the fact that the same introduction I have made here is presented very differently if you study it in the ordinary textbooks of physics. I will not well you how it is presented in the average textbook of physics. It would be said: \(\alpha\) is a ratio. It is a fraction. The expansion is relatively very small as compared to the original length of the rod. When I have a fraction whose denominator is greater than its numerator, then when I square or cube it, I get a much smaller fraction. For if I square a third, I get a ninth and when I cube a third I get a twenty-seventh. That is, the third power is a very, very small fraction. \(\alpha\) is a fraction whose denominator is usually very large. Therefore say most physics books: if I square \(\alpha\) to get \(\alpha^2\) or cube it to get \(\alpha^3\) with which I multiply \(t^3\) these are very small fractions and can simply be dropped out. The average physics text says: we simply drop these last terms of the expansion formula and write \(l \cdot b \cdot d\)—this is the volume and I will write is as \(V\)—the volume of an expanded body heated to a certain temperature is:
$$V=V_o(1 + 3 \alpha t) \qquad (7)$$[ 12 ] In this fashion is expressed the formula for the expansion of a solid body. It is simply considered that since the fraction \(\alpha\) squared and cubed give such small quantities, these can be dropped out. You recognize this as the treatment in the physics texts. Now my friends, in doing this, the most important thing for a really informative theory of heat is stricken out. This will appear as we progress further. [ 14 ] Expansion under the influence of heat is shown not only by solids but by fluids as well. Here we have a fluid colored so that you can see it. We will warm this colored fluid (See Figure 1b). Now you notice that after a short time the colored fluid rises and from that we can conclude that fluids expand just like solids. Since the colored fluid rises, therefore fluids expand when warmed.
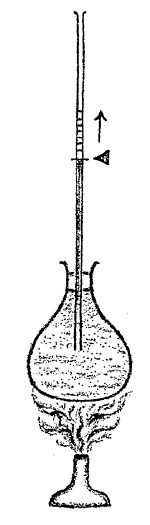
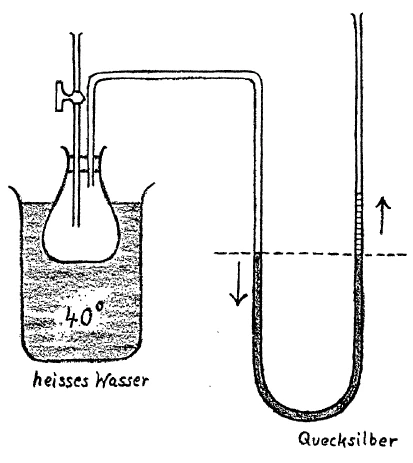
[ 14 ] Now we can in the same way investigate the expansion of a gaseous body. For this purpose we have here a vessel filled simply with air. (See Figure 2). We shut off the air in the vessel and warm it. Notice that here is a tube communicating with the vessel and containing a liquid whose level is the same in both arms of the tube. When we simply warm the air in the vessel, which air constitutes a gaseous body, you will see what happens. We will warm it by immersing the vessel in water heated to a temperature of 40°. (Note: temperatures in the lectures are given in degrees Celsius.) You will see, the mercury at once rises. Why does it rise? Because the gaseous body in the vessel expands. The air streams into the tube, presses on the mercury and the pressure forces the mercury column up into the tube. From this you see that the gaseous body has expanded. We may conclude that solid, liquid and gaseous bodies all expand under the influence of the being of heat, as yet unknown to us.
[ 15 ] Now, however, a very important matter approaches us when we proceed from the study of the expansion of solids through the expansion of liquids to the expansion of a gas. I have already stated that \(\alpha\), the relation of the expansion to the original length of the rod, differed for different substances. If by means of further experiments that cannot be performed here, we investigate \(\alpha\) for various fluids, again we will find different values for various fluid substances. When however, we investigate \(\alpha\) for gaseous bodies then a peculiar thing shows itself, namely that \(\alpha\) is not different for various gases but that this expansion coefficient as it is called, is the same and has a constant value of about \(\frac{1}{273}\). This fact is of tremendous importance. From it we see that as we advance from solid bodies to gases, genuinely new relations with heat appear. It appears that different gases are related to heat simply according to their property of being gases and not according to variations in the nature of the matter composing them. The condition of being a gas is, so to speak, a property which may be shared in common by all bodies. We see indeed, that for all gases known to us on earth, the property of being a gas gathers together into a unity this property of expanding. Keep in mind now that the facts of expansion under the influence of heat oblige us to say that as we proceed from solid bodies to gases, the different expansion values found in the case of solids are transformed into a kind of unity, or single power of expansion for gases. Thus if I may express myself cautiously, the solid condition may be said to be associated with an individualization of material condition. Modern physics pays scant attention to this circumstance. No attention is paid to it because the most important things are obscured by the fact of striking out certain values which cannot be adequately handled.
[ 16 ] The history of the development of physics must be called in to a certain extent in order to gain insight into the things involved in a deeper insight into these matters. All the ideas current in the modern physics texts and ruling the methods by which the facts of physics are handled are really not old. They began for the most part in the 17th century and took their fundamental character from the new impulse given by a certain scientific spirit in Europe through Academia del Cimento in Florence. This was founded in 1667 and many experiments in quite different fields were carried out there, especially however, experiments dealing with heat, acoustics and tone. How recent our ordinary ideas are may be realized when we look up some of the special apparatus of the Academia del Cimento. It was there for instance, that the ground work for our modern thermometry was laid. It was at this academy that there was observed for the first time how the mercury behaves in a glass tube ending at the bottom in a closed cylinder, when the mercury filling the tube is warmed. Here, in the Academia del Cimento, it was first noticed that there is an apparent contradiction between the experiments where the expansion of liquids may be observed and another experiment. The generalization had been attained that liquids expand. But when the experiment was carried out with quicksilver it was noticed that it first fell when the tube was heated and after that began to rise. This was first explained in the 17th century, and quite simply, by saying: When heat is applied, the outer glass is heated at the start and expands. The space occupied by the quicksilver becomes greater. It sinks at first, and begins to rise only when the heat has penetrated into the mercury itself. Ideas of this sort have been current since the 17th century. At the same time, however, people were backward in a grasp of the real ideas necessary to understand physics, since this period, the Renaissance, found Europe little inclined to trouble itself with scientific concepts. It was the time set aside for the spread of Christianity. This in a certain sense, hindered the process of definite physical phenomena. For during the Renaissance, which carried with it an acquaintance with the ideas of ancient Greece, men were in somewhat the following situation. On the one hand encouraged by all and every kind of support, there arose institutions like the Academia del Cimento, where it was possible to experiment. The course of natural phenomena could be observed directly. On the other hand, people had become unaccustomed to construct concepts about things. They had lost the habit of really following things in thought. The old Grecian ideas were now taken up again, but they were no longer understood. Thus the concepts of fire or heat or as much of them as could be understood were assumed to be the same as were held by the ancient Greeks. And at this time was formed that great chasm between thought and what can be derived from the observation of experiments. This chasm has widened more and more since the 17th century. The art of experiment reached its full flower in the 19th century, but a development of clear, definite ideas did not parallel this flowering of the experimental art. And today, lacking the clear, definite ideas, we often stand perplexed before phenomena revealed in the course of time by unthinking experimentation. When the way has been found not only to experiment and to observe the outer results of the experiments but really to enter into the inner nature of the phenomena, then only can these results be made fruitful for human spiritual development.
[ 17 ] Note now, when we penetrate into the inner being of natural phenomena then it becomes a matter of great importance that entirely different expansion relations enter in when we proceed from solids to gases. But until the whole body of our physical concepts is extended we will not really be able to evaluate such things as we have today drawn plainly from the facts themselves. To the facts, already brought out, another one of extraordinary importance must be added.
[ 18 ] You know that a general rule can be stated as we have already stated it, namely if bodies are warmed they expand. If they are cooled again they contract. So that in general the law may be stated: “Through heating, bodies expand; through cooling they contract.” But you will recollect from your elementary physics that there are exceptions to this rule, and one exception that is of cardinal importance is the one in regard to water. When water is made to expand and contract, then a remarkable fact is come upon. If we have water at 80° say, and we cool it, it first contracts. That goes without saying, as it were. But when the water is cooled further it does not contract but expands again. Thus the ice that is formed from water—and we will speak further of this—since it is more expanded and therefore less dense than water, floats on the surface of the water. This is a striking phenomenon, that ice can float on the surface of the water! It comes about through the fact that water behaves irregularly and does not follow the general law of expansion and contraction. If this were not so, if we did not have this exception, the whole arrangement of nature would be peculiarly affected. If you observe a basin filled with water or a pond, you will see that even in the very cold winter weather, there is a coating of ice on the surface only and that this protects the underlying water from further cooling. Always there is an ice coating and underneath there is protected water. The irregularity that appears here is, to use a homely expression, of tremendous importance in the household of nature. Now the manner of forming a physical concept that we can depend on in this case must be strictly according to the principles laid down in the last course. We must avoid the path that leads to an Achilles-and-the-turtle conclusion. We must not forget the manifested facts and must experiment with the facts in mind, that is, we must remain in the field where the accessible facts are such as to enable us to determine something. Therefore, let us hold strictly to what is given and from this seek an explanation for the phenomena. We will especially hold fast to such things, given to observation, as expansion and irregularity in expansion like that of water (noting that it is associated with a fluid.) Such factual matters should be kept in mind and we must remain in the world of actualities. This is real Goetheanism.
[ 19 ] Let us now consider this thing, which is not a theory but a demonstrable fact of the outer world. When matter passes into the gaseous condition there enters in a unification of properties for all the substances on the earth and with the passage to the solid condition there takes place an individualizing, a differentiation.
Now if we ask ourselves how it can come about that with the passage from the solid to the gaseous through the liquid state a unification takes place, we have a great deal of difficulty in answering on the basis of our available concepts. We must first, if we are to be able to remain in the realm of the demonstrable, put certain fundamental questions. We must first ask: Whence comes the possibility for expansion in bodies, followed finally by change into the gaseous state with its accompanying unification of properties?
You have only to look in a general way at all that is to be known about the physical processes on the earth in order to come to the following conclusion: Unless the action of the sun were present, we could not have all these phenomena taking place through heat. You must give attention to the enormous meaning that the being of the sun has for the phenomena of earth. And when you consider this which is simply a matter of fact, you are obliged to say: this unification of properties that takes place in the passage from the solid through the fluid and into the gaseous state, could not happen if the earth were left to itself. Only when we go beyond the merely earthly relations can we find a firm standpoint for our consideration of these things. When we admit this, however, we have made a very far reaching admission. For by putting the way of thinking of the Academia del Cimento and all that went with it in place of the above mentioned point of view, the old concepts still possible in Greece were robbed of all their super-earthly characteristics. And you will soon see, that purely from the facts, without any historical help, we are going to come back to these concepts. It will perhaps be easier to win way into your understanding if I make a short historical sketch at this time.
[ 20 ] I have already said that the real meaning of those ideas and concepts of physical phenomena that were still prevalent in ancient Greece have been lost. Experimentation was started and without the inner thought process still gone through as in ancient Greece, ideas and concepts were taken up parrot-fashion, as it were. Then all that the Greeks included in these physical concepts was forgotten. The Greeks had not simply said, “Solid, liquid, gaseous,” but what they expressed may be translated into our language as follows:
Whatever was solid was called in ancient Greek earth;
Whatever was fluid was called in ancient Greece water;
Whatever was gaseous was called in ancient Greece air.
[ 21 ] It is quite erroneous to think that we carry our own meaning of the words earth, air and water over into old writings where Grecian influence was dominant, and assume that the corresponding words have the same meaning there. When in old writings, we come across the word water we must translate it by our word fluid; the word earth by our words solid bodies. Only in this way can we correctly translate old writings. But a profound meaning lies in this. The use of the word earth to indicate solid bodies implied especially that this solid condition falls under the laws ruling on the planet earth. (As stated above, we will come upon these things in following lectures from the fact themselves; they are presented today in this historical sketch simply to further your understanding of the matter.)
Solids were designated as earth because it was desired to convey this idea: When a body is solid it is under the influence of the earthly laws in every respect. On the other hand, when a body was spoken of as water, then it was not merely under the earthly laws but influenced by the entire planetary system. The forces active in fluid bodies, in water, spring not merely from the earth, but from the planetary system. The forces of Mercury, Mars, etc. are active in all that is fluid. But they act in such a way that they are oriented according to the relation of the planets and show a kind of resultant in the fluid.
[ 22 ] The feeling was, thus, that only solid bodies, designated as earth, were under the earthly system of laws; and that when a body melted it was influenced from outside the earth. And when a gaseous body was called air, the feeling was that such a body was under the unifying influence of the sun, (these things are simply presented historically at this point,) this body was lifted out of the earthly and the planetary and stood under the unifying influence of the sun. Earthly air being were looked upon in this way, that their configuration, their inner arrangement and substance were principally the field for unifying forces of the sun.
You see, ancient physics had a cosmic character. It was willing to take account of the forces actually present in fact. For the Moon, Mercury, Mars, etc. are facts. But people lost the sources of this view of things and were at first not able to develop a need for new sources. Thus they could only conceive that since solid bodies in their expansion and in their whole configuration fell under the laws of the earth, that liquid and gaseous bodies must do likewise. You might say that it would never occur to a physicist to deny that the sun warmed the air, etc. He does not, indeed do this, but since he proceeds from concepts such as I characterized yesterday, which delineate the action of the sun according to ideas springing from observations on the earth, he therefore explains the sun in terrestrial terms instead of explaining the terrestrial in solar terms.
[ 23 ] The essential thing is that the consciousness of certain things was completely lost in the period extending from the 15th to the 17th centuries. The consciousness that our earth is a member of the whole solar system and that consequently every single thing on the earth had to do with the whole solar system was lost. Also there was lost the feeling that the solidity of bodies arose, as it were, because the earthly emancipated itself from the cosmic, that it tore itself free to attain independent action while the gaseous, for example, the air, remained in its behavior under the unifying influence of the sun as it affected the earth as a whole. It is this which has led to the necessity of explaining things terrestrially which formerly received a cosmic explanation. Since man no longer sought for planetary forces acting when a solid body changes to a fluid, as when ice becomes fluid—changes to water—since the forces were no longer sought in the planetary system, they had to be placed within the body itself. It was necessary to rationalize and to theorize over the way in which the atoms and molecules were arranged in such a body. And to these unfortunate molecules and atoms had to be ascribed the ability from within to bring about the change from solid to liquid, from liquid to gas. Formerly such a change was considered as acting through the spatially given phenomena from the cosmic regions beyond the earth. It is in this way we must understand the transition of the concepts of physics as shown especially in the crass materialism of the Academia del Cimento which flowered in the ten year period between 1657 and 1667. You must picture to yourselves that this crass materialism arose through the gradual loss of ideas embodying the connection between the earthly and the cosmos beyond the earth. Today the necessity faces us again to realize this connection. It will not be possible, my friends, to escape from materialism unless we cease being Philistines just in this field of physics. The narrow-mindedness comes about just because we go from the concrete to the abstract, for no one loves abstractions more than the Philistine. He wishes to explain everything by a few formulae, a few abstract ideas. But physics cannot hope to advance if she continues to spin theories as has been the fashion ever since the materialism of the Academia del Cimento. We will only progress in such a field as that of the understanding of heat if we seek again to establish the connection between the terrestrial and the cosmic through wider and more comprehensive ideas than modern materialistic physics can furnish us.
Zweiter Vortrag
[ 1 ] Schon gestern wurde berührt, daß unter dem Einfluß des Wärmewesens sich dasjenige, was wir im gewöhnlichen Leben Körper nennen, ausdehnt. Wir wollen heute zunächst davon ausgehen, wie sich sogenannte feste Körper unter dem Einfluß des Wärmewesens ausdehnen. Wir haben zu diesem Zweck hier, damit wir uns die Dinge auch einprägen und sie dann auch in entsprechender Weise im Unterricht verwerten können — es ist ja einfach und elementar zunächst -, eine Eisenstange eingespannt. Diese Eisenstange wollen wir erhitzen und ihre Ausdehnung anschaulich machen dadurch, daß hier an dieser Marke der Hebelarm, der hier angebracht ist, die Längenänderung anzeigen wird. Wenn ich hier mit dem Finger drücke, so bewegt sich dieser Zeiger nach aufwärts.

[ 2 ] Sie werden sehen, daß, wenn wir diesen Stab hier erhitzen, sich dieser Zeiger ebenfalls aufwärts bewegen wird, was Ihnen ein Beweis sein wird, daß der Stab sich ausdehnt. Sie sehen schon, wie der Zeiger nach aufwärts rückt. Und Sie sehen, daß mit der fortgehenden Erwärmung der Zeiger mehr und mehr nach aufwärts rückt, was Ihnen ein Beweis ist, daß die Ausdehnung mit der Temperatur wächst. Würde ich statt der Substanz dieses Körpers irgendein anderes Metall verwendet haben und wir würden dann genau messen, so würden wir eine andere Ausdehnung bekommen. Wir würden finden, daß verschiedene solche Körper sich in verschieden starker Weise ausdehnen. So daß wir zunächst zu konstatieren hätten, daß die Ausdehnungsfähigkeit, die Stärke der Ausdehnung von der Substanz abhängt. Wir sehen zunächst hier ab davon, daß wir eigentlich einen Zylinder vor uns haben. Wir stellen uns zunächst vor, daß wir einfach einen Körper von einer bestimmten Länge ohne Dicke und Breite vor uns haben, und wir beobachten zunächst die Ausdehnung nur nach einer Dimension. Wenn wir uns das veranschaulichen, so bekommen wir folgendes:

[ 3 ] Wenn hier ein Stab festgehalten wird, und wir ihn nur eigentlich als eine Länge betrachten, wollen wir zunächst für die Temperatur, den Wärmegrad, von dem wir ausgehen, die Länge dieses Stabes mit \(l_0\) bezeichnen. Und wir bezeichnen dann die Länge des Stabes, die er bekommt, wenn wir seine Temperatur zunächst um 1 Grad erhöhen mit \(l\). Nun sagte ich, daß die Stäbe sich verschieden stark ausdehnen, je nachdem sie von der einen oder anderen Substanz sind. Wir können nun immer das Maß der Ausdehnung, also hier von \(a\) nach \(b\), uns angeben durch einen Bruch, der das Verhältnis der Ausdehnung zu der ursprünglichen Stablänge bezeichnet. Wir wollen das, also diese verhältnismäßige Stärke der Ausdehnung, mit \(\alpha\) bezeichnen. Dann haben wir die Länge, die der Stab hat, nachdem er sich ausgedehnt hat, also die Länge \(l\), uns zusammengesetzt zu denken aus seiner ursprünglichen Länge \(l_0\) und aus dem Stückchen, das er in seiner Länge hinzubekommen hat durch die Ausdehnung. Dieses müssen wir dazurechnen. Dadurch, daß ich \(\alpha\) als Bruch bezeichnet habe, der das Verhältnis angibt zwischen der Ausdehnung und der ursprünglichen Länge, dadurch bekomme ich, indem ich \(l_0\) mit \(\alpha\) multipliziere, die Tendenz der Ausdehnung des Stabes, und ich habe, weil ja die Ausdehnung um so bedeutender wird, je höher die Temperatur wird, das zu multiplizieren mit der Temperaturzunahme \(t\). So daß ich sagen kann: Die Stablänge \(l\) nach der Ausdehnung
$$l = l_0 + l_0 \alpha t = l_0(1 + \alpha t)$$
[ 4 ] Das heißt, will ich feststellen die Länge eines Stabes, der sich durch Erwärmung ausgedehnt hat, so muß ich seine ursprüngliche Länge mit einem Faktor multiplizieren, der hier angegeben wird durch 1 plus die Temperatur, multipliziert mit der verhältnismäßigen Ausdehnungsfähigkeit der betreffenden Substanz. Die Physiker sind gewohnt worden, das \(\alpha\) für die betreffende Substanz den Ausdehnungskoeffizienten zu nennen.

[ 5 ] Nun habe ich hier einen Stab betrachtet. Stäbe von keiner Breite und keiner Höhe haben wir in Wirklichkeit nicht. Wir haben in Wirklichkeit ja Körper von drei Dimensionen. Wir können, wenn wir nun übergehen von dieser Längenausdehnung zunächst wiederum zur nur gedachten Flächenausdehnung, diese Formel in der folgenden Weise umwandeln: Nehmen wir an, wir betrachten statt wie hier die Längenausdehnung nun die Flächenausdehnung. Hätten wir also hier eine Fläche, so müßten wir uns klar sein, daß die Fläche sich ausdehnt nach zwei Dimensionen, also nach der Erwärmung etwa diese Größe hätte. Wir hätten dann nicht nur die Längenausdehnung nach |, sondern auch die Breitenausdehnung nach \(b\). Und wenn wir die Längenausdehnung zuerst betrachten, hier \(l_0\), so würden wir haben wiederum die Ausdehnung nach dieser Richtung, die ich jetzt angegeben habe, nach \(l\). Und wir haben
$$l = l_0(1 + \alpha t). \qquad (1)$$
[ 6 ] Betrachten wir jetzt auch die Breitenausdehnung \(b_0\), die sich ausgedehnt hat zu \(b\), so müßte ich jetzt schreiben — es ist ja selbstverständlich, daß das Ausdehnungsgesetz dasselbe bleibt —
$$b = b_0(1 + \alpha t) \qquad (2)$$
[ 7 ] Nun wissen Sie, daß die Fläche sich ergibt, indem ich die Länge mit der Breite multipliziere. Ich bekomme also den ganzen Inhalt der Fläche, der hier der ursprüngliche ist, indem ich \(b_0\), mit \(l_0\), multipliziere, und hier denjenigen nach der Ausdehnung, indem ich auch nun \(l_0(1 + \alpha t)\) multipliziere mit \(b_0(1 + \alpha t)\).
$$lb = l_0(l + \alpha t)b_0(1 + \alpha t) \qquad (3)$$
Das heißt, ich bekomme:
$$lb = l_0b_0 (1 + \alpha t)^2 \qquad (4)$$
das heißt aber ausgeschrieben:
$$lb = l_0b_0 (1 + 2\alpha t + \alpha^2 t^t) \qquad (5)$$
[ 8 ] Damit würde ich die Formel haben für die Ausdehnung einer Fläche.
[ 9 ] Wenn Sie sich nun zu der Fläche noch hinzudenken eine Dicke, so habe ich diese Dicke in derselben Weise zu behandeln. Ich würde dann noch d hinzuzufügen haben und erhalte:
$$ lbd = l_0b_0d_0(1 + 3\alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3). \qquad (6)$$[ 10 ] Und wenn Sie diese Formel anschauen, dann bitte ich Sie besonders im Auge zu behalten das Folgende: Wenn wir hier die ersten zwei Glieder dieser Formel (6) betrachten, dann werden Sie das t höchstens in der ersten Potenz finden. Wenn Sie das dritte Glied betrachten, finden Sie das t in der zweiten Potenz, und das letzte t in der dritten Potenz. Diese beiden letzten Glieder der Formel für die Ausdehnung bitte ich Sie ganz besonders zu berücksichtigen. Merken Sie sich, daß, wenn wir die Ausdehnung eines dreidimensionalen Körpers haben, wir für diesen einen Formelausdruck bekommen, der die dritte Potenz der Temperatur enthält - ich will etwas absehen von der zweiten Potenz der Temperatur. Es ist außerordentlich wichtig, daß gerade festgehalten werde an diesem Umstand, daß wir hier die dritte Potenz der Temperatur bekommen.
[ 11 ] Da ich immer Rücksicht darauf nehmen muß, daß wir ja hier in der Waldorfschule sind und alles auch auf das Pädagogische hin orientiert sein muß, ist es nötig, Sie darauf aufmerksam zu machen, daß wenn Sie nun dieselbe Herleitung, die ich hier gemacht habe, in den gebräuchlichen Handbüchern der Physik studieren, Sie in der Art, wie ich hier die Sache dargestellt habe, einen beträchtlichen Unterschied zu der Schilderung in den gebräuchlichen Handbüchern der Physik finden werden. Ich will Ihnen jetzt mitteilen, wie die Darstellung in den gebräuchlichen Handbüchern der Physik gegeben wird. Da wird gesagt: « ist eine Verhältniszahl — es ist ja in der Regel ein Bruch. Die Ausdehnung ist sehr klein im Verhältnis zu der ursprünglichen Länge des Stabes. Wenn ich einen Bruch habe, der im Nenner eine größere Zahl hat als im Zähler, dann bekomme ich, wenn ich quadriere oder kubiere, eine viel kleinere Zahl. Denn quadriere ich ein Drittel, so bekomme ich schon ein Neuntel, und kubiere ich gar ein Drittel, so bekomme ich ein Siebenundzwanzigstel. Das heißt, die dritte Potenz ist schon ein sehr, sehr kleiner Bruch. «& ist ein Bruch, der einen sehr großen Nenner hat in der Regel. Deshalb sagen die gebräuchlichen Handbücher der Physik: Wenn ich nun das Quadrat bilde, \(\alpha^2\) oder gar \(\alpha^3\), mit dem ich zu multiplizieren habe das \(t^3\), so sind das sehr kleine Brüche, die kann man einfach weglassen. So daß also die gebräuchlichen Handbücher der Physik sagen: Wir lassen diese letzten Glieder der Ausdehnungsformel einfach weg und schreiben \(l \cdot b \cdot d\) — das ist ja das Volumen, das ein sich ausdehnender Körper durch eine bestimmte Temperatur annimmt, ich will also \(V\) schreiben -:
$$V = V_0(1 + 3 \alpha t). \qquad (7)$$
[ 12 ] In dieser Art wird die Formel geschrieben für die Ausdehnung eines festen Körpers, indem man sich einfach darauf beruft, daß der Bruch \(\alpha\) quadriert und namentlich kubiert so kleine Zahlen gibt, daß man diese weglassen kann. Sie wissen, so ist es dargestellt in den gebräuchlichen Physikbüchern. Nun, damit streicht man weg das Allerwichtigste, worauf es ankommt, wenn man nun wirklich sachgemäß Wärmelehre treiben will. Das wird sich uns zeigen, indem wir weiter vorrücken.

[ 13 ] Ausdehnung durch das Wärmewesen haben ja nicht nur die festen Körper, sondern auch die Flüssigkeiten. Sie haben hier, damit Sie es i sehen können, eine gefärbte Flüssigkeit. Wir werden diese gefärbte Flüssigkeit erwärmen (siehe Zeichnung). Sie werden nun sehen, daß nach einiger Zeit die gefärbte Flüssigkeitssäule in die Höhe steigt, und daraus werden Sie entnehmen, daß Flüssigkeiten sich ebenso ausdehnen wie feste Körper. Sie sehen, die gefärbte Flüssigkeit steigt, also die Flüssigkeit dehnt sich aus durch Erwärmung.
[ 14 ] Nun, ebenso können wir untersuchen die Ausdehnung eines luftförmigen Körpers. Dazu haben wir hier in dem Kolben Luft, die einfach von außen hineinkommt (siehe Zeichnung). Wir schließen nun die im Kolben befindliche Luft ab und erwärmen diese Luft. Wir haben hier ein kommunizierendes Gefäß. Die Eigenschaft der kommunizierenden Gefäße ist ja, daß das Niveau der Flüssigkeit, die darin ist, auf beiden Seiten gleich ist, also beide Sehenkel umfaßt. Sie werden nun sehen, was geschieht, wenn wir einfach die hier drinnen befindliche Luft, also einen luftförmigen Körper, erhitzen. Wir werden es dadurch erreichen, daß in dem Gefäß (siehe Zeichnung Seite 36) erwärmtes Wasser ist von einer Temperatur von 40°. Sie sehen, schon rückt rechts die Quecksilbersäule hinauf. Warum rückt sie hinauf? Weil der luftförmige Körper, der in diesem Kolben hier ist, sich ausdehnt. Die Luft strömt hier heraus, drückt auf dieses Quecksilber (links), auf der anderen Seite wird die Quecksilbersäule durch den Druck gehoben, und Sie sehen daraus, daß dieser luftförmige Körper sich ausgedehnt hat. So daß wir also sagen können: Sowohl feste, wie flüssige, wie luftförmige Körper dehnen sich durch Einwirkung des uns noch unbekannten Wärmewesens aus.

[ 15 ] Nun aber tritt uns hier sogleich, wenn wir vorrücken von dem Studium der Ausdehnung bei festen Körpern, durch das Studium der Ausdehnung bei Flüssigkeiten zu dem Studium der Ausdehnung bei luftförmigen Körpern, etwas sehr Bedeutsames entgegen. Ich habe früher gesagt, daß das « hier, die Verhältniszahl der Ausdehnung zur ursprünglichen Länge des Stabes, für verschiedene Substanzen verschieden ist. Wenn wir, was ja weitere Experimente in Anspruch nehmen würde, die wir hier nicht ausführen können, nun auch das \(\alpha\) untersuchen würden für verschiedene Flüssigkeiten, würden wir noch für das \(\alpha\) verschiedene Werte bekommen für verschiedene Flüssigkeitssubstanzen. Wenn wir aber das \(\alpha\) untersuchen für luftförmige Körper, namentlich für Gase, so zeigt sich das Eigentümliche, daß nun das « nicht mehr für verschiedene luftförmige Körper verschieden ist, sondern daß das \(\alpha\), der Ausdehnungskoeffizient, wie man es nennt, für die verschiedenen Gase dasselbe ist, nämlich annähernd \(\frac{1}{273}\). Diese Tatsache ist von einer ganz eminenten Wichtigkeit. Wir sehen daraus, daß, indem wir vorrücken von den festen Körpern zu den luftförmigen Körpern, eigentlich neue Verhältnisse unter dem Einfluß des Wärmewesens eintreten. Wir sehen daraus, daß sich die verschiedenen Gase nicht verhalten nach ihrer verschiedenen Substantialität, sondern daß sie sich verhalten dem Wärmewesen gegenüber einfach nach ihrer Eigenschaft, Gase zu sein, daß das Gaswerden etwas ist, was gewissermaßen als eine gemeinschaftliche Eigenschaft über alle Körper kommen kann. Ja, wir sehen daraus, daß das Gaswerden etwas ist, was alle Gase, die uns im irdischen Umkreis bekannt werden können, wenigstens in bezug auf diese Eigenschaft ihrer Ausdehnungsfähigkeit, zu einer Einheit zusammenfaßt. Halten Sie fest, daß wir einfach an der Ausdehnungsfähigkeit durch die Wärme dazu kommen, sagen zu müssen, daß sich, indem man sich von den festen Körpern her den Gasen nähert, die differenzierte Ausdehnungsfähigkeit, die wir bei festen Körpern finden, in eine Art Einheit, in eine einheitliche Ausdehnungsfähigkeit umwandelt bei Gasen, daß also mit dem festen Zustand verknüpft ist in unserem irdischen Bereich eine Differenzierung der Körperlichkeiten, wenn ich mich vorsichtig ausdrücke. Ich könnte auch sagen, daß verknüpft ist mit dem Festwerden eine Individualisierung der Körperlichkeit. Auf diesen Umstand wird sehr wenig hingewiesen in der neueren Physik. Es wird nicht darauf hingewiesen, weil man wichtigste Dinge einfach dadurch kaschiert, daß man gewisse Größen wegstreicht, mit denen man nichts Rechtes anfangen kann.
[ 16 ] Tiefer hineinsehen in dasjenige, um was es sich da handelt, kann man nur dann, wenn man ein wenig zu Hilfe ruft die Geschichte der physikalischen Entwickelung. Alle die Vorstellungen, die heute in Physikbüchern und überhaupt in der Behandlung der Physik herrschend sind, sind ja im Grunde genommen noch nicht alt. Sie rühren im wesentlichen aus dem 17. Jahrhundert her, und zwar haben sie ihren Grundcharakter bekommen durch alles dasjenige, was man im 17. Jahrhundert unter dem Neuaufleben eines gewissen wissenschaftlichen Geistes in Europa veranstaltet hat durch die Accademia del Cimento in Florenz, die 1657 gegründet worden ist und in der außerordentlich viele Experimente auf den verschiedensten Gebieten gemacht worden sind, namentlich aber auf dem Gebiete des Wärmewesens, auf dem Gebiete der Akustik, des Tonwesens und so weiter. Wie jung unsere gebräuchlichen Vorstellungen sind auf diesem Gebiete, das zeigt sich ja, wenn man ein wenig eingeht auf gewisse spezielle Veranstaltungen der Accademia del Cimento. Da wurde zum Beispiel zuerst eigentlich die Grundlage gelegt für unsere moderne Thermometrie. Da wurde zuerst bemerkt, wie in einer Glasröhre, die unten mit einem Zylinder abgeschlossen ist, was Sie ja an jedem Thermometer sehen können, wie da die Erwärmung auf Quecksilber, mit dem die Glasröhre gefüllt ist, wirkt. Da wurde man zum Beispiel erst aufmerksam darauf, daß ein scheinbarer Widerspruch besteht zwischen der Anschauung, die man sonst gewonnen hat, also etwa durch ein solches Experiment, wo eine Flüssigkeit sich einfach ausdehnt, und dem, was sich besonders stark zeigte, indem man einen Versuch, der belehrend sein sollte, machte. Man war so im allgemeinen zu der. Anschauung gekommen: Flüssigkeiten dehnen sich auch aus. Aber indem man den Versuch anstellte mit Quecksilber, fiel es zunächst unter der Erwärmung, und dann erst stieg es. Man mußte dafür erst eine Erklärung im 17. Jahrhundert finden, die man ja leicht dafür finden konnte dadurch, daß man sich sagte: Wenn ich erhitze, so erhitze ich zunächst das äußere Glas. Das dehnt sich aus. Der Raum, den das Quecksilber ausfüllt, wird größer; es sinkt zuerst, und der innere Körper beginnt erst etwas zu steigen, wenn die Erwärmung nach dem Inneren vorgedrungen ist. — Solche Begriffe bekam man überhaupt erst seit dem 17. Jahrhundert. Aber mit diesem 17. Jahrhundert war man auch gegenüber all den Ideen, durch die man das Physikalische zu begreifen versuchen sollte, dadurch gar sehr in Rückstand gekommen, daß sich ja bis zu dieser Zeit, zur eigentlichen Renaissance, Europa so wenig gekümmert hat um wissenschaftliche Begriffe dieser Art. Es war die Zeit, in der sich hat ausbreiten müssen das Christentum, das in einer gewissen Weise verhindert hat, daß Begriffe sich festlegen konnten, sich ausbilden konnten über physikalische Erscheinungen. Dann, als die Renaissance kam, als man bekannt wurde mit den Vorstellungen, die im alten Griechenland schon da waren, war man etwa in der folgenden Lage: Auf der einen Seite, aufgemuntert durch allerlei bereitwillige Unterstützungen, bildeten sich solche Institute wie die Accademia del Cimento, und da konnte man nun experimentieren. Man konnte unmittelbar anschaulich machen, wie die physikalischen Erscheinungen verlaufen. Auf der anderen Seite aber wurde man entwöhnt, sich Begriffe zu machen über die Dinge. Man wurde entwöhnt, die Erscheinungen wirklich denkend zu verfolgen. Man nahm wieder die alten griechischen Vorstellungen, die jetzt vielfach wie aufgefangen wurden, auf, aber man verstand sie nicht mehr. Und so nahm man auch die Vorstellung von Feuer oder Wärme, ohne irgendwie das unter diesem Begriff verstehen zu können, was man im alten Griechenland darunter verstanden hat. Und es bildete sich jetzt jene tiefe Kluft zwischen dem Denken und dem, was für die Anschauung durch das Experiment gegeben werden kann. Diese Kluft tat sich immer mehr und mehr auf gerade seit dem 17. Jahrhundert. Die Experimentierkunst wurde dann besonders im 19. Jahrhundert vervollkommnet, aber klare, deutliche Begriffe gingen nicht parallel dieser Vervollkommnung der Experimentierkunst. Und heute stehen wir, indem uns solche klare, deutliche, anschaubare Begriffe fehlen, vielfach vor jenen Erscheinungen ratlos, die das gedankenlose Experimentieren im Lauf der Zeit hervorgebracht hat und die im weiteren sich nur fruchtbar der menschlichen Geistesentwickelung einverleiben können, wenn wiederum der Weg gefunden wird, nicht nur zu experimentieren und den Verlauf des Experiments äußerlich anzuschauen, sondern in den inneren Gang des Naturgeschehens wirklich einzutreten.
[ 17 ] Sehen Sie, beim Eindringen in den inneren Gang des Naturgeschehens kommt dann so etwas außerordentlich stark in Betracht, daß in bezug auf die Ausdehnungsfähigkeit vollständig neue Verhältnisse eintreten, wenn wir von den festen Körpern zu den Gasen hinaufdringen. Aber man wird niemals ohne die Erweiterung unseres ganzen physikalischen Vorstellungslebens solche Dinge, wie sie heute eigentlich den Tatsachen nach schon vorliegen, wirklich bewältigen können. Zu diesen Tatsachen, die wir schon angeführt haben, kommt ja noch eine andere, die außerordentlich bedeutsam ist.
[ 18 ] Nicht wahr, wie eine allgemeine Regel kann man sich bilden aus dem, was wir jetzt schon hier dargestellt haben, den Satz: Erwärmen wir Körper, so dehnen sie sich aus; erkalten sie dann wiederum, so ziehen sie sich zusammen. So daß der allgemeine Satz gebildet werden könnte: Durch Erwärmung dehnen sich Körper aus, durch Erkaltung ziehen sich Körper zusammen. Nun wissen Sie aber aus der elementaren Physik, daß es von diesem Satz Ausnahmen gibt, vor allen Dingen eine Kardinalausnahme, die bezüglich des Wassers selber. Wenn man Wasser zur Ausdehnung bringt und zum Wiederzusammenziehen, so zeigt sich das Merkwürdige, daß, wenn man Wasser von einer Temperatur von 8° hat und es dann erkaltet, es sich zusammenzieht. Das ist selbstverständlich, möchte ich sagen. Aber wenn man dann weiter abkühlt, zieht es sich nicht zusammen, sondern dehnt sich wieder aus. So daß Eis, das aus dem Wasser entsteht - wir werden über diese Entstehung noch zu sprechen haben -, weil es ausgedehnter und damit weniger dicht ist als das Wasser, auf dem Wasser schwimmen kann. Eine eigentümliche Erscheinung,. daß Eis auf dem Wasser schwimmen kann! Sie rührt davon her, daß dieses allgemeine Gesetz der Ausdehnbarkeit und Zusammenziehbarkeit eben für das Wasser eine Unregelmäßigkeit aufweist, daß das Wasser im allgemeinen diesem Gesetz nicht so ohne weiteres folgt. Es wäre ja auch mit unserer ganzen Natureinrichtung eigentümlich bestellt, wenn das anders wäre, wenn diese Ausnahme nicht bestünde. Wenn Sie ein Bassin, einen Teich und so weiter beobachten, so werden Sie sehen, daß selbst bei strengem Winter nur eine Eisdecke da ist, und das Wasser nicht bis unten gefriert. Daß unten das Wasser ungefroren bleibt, das geschieht aus dem Grunde, weil das sich oben zunächst bildende Eis schwimmt und dadurch eine Decke bildet, und daß dadurch das darunter befindliche Wasser vor der weiteren Abkühlung bewahrt bleibt. Sie haben immer oben eine Eisdecke und unten ein geschütztes Wasser. Diese Unregelmäßigkeit, die hier auftritt, hängt also mit etwas zusammen, was eigentlich — wenn ich den etwas spießbürgerlichen Ausdruck gebrauchen darf — mit dem Haushalt unserer Natur außerordentlich viel zu tun hat. Nun, sehen Sie, die physikalische Betrachtungsweise, zu der wir hier unsere Zuflucht nehmen wollen, die muß durchaus so sein, wie ich es beim letzten Kursus schon angedeutet habe. Wir müssen es vermeiden, den Weg zu dem Achilles-und-der-Schildkröte-Schluß hin zu machen. Wir müssen es vermeiden, abzusehen von dem Anschaulichen, wir müssen durchaus den Versuch machen, im Anschaulichen, das heißt, in dem mit der Anschauung Konstatierbaren zu verbleiben. Daher werden wir uns immer streng an das Anschauliche halten und versuchen, aus dem Anschaulichen heraus eine Erklärung für die Erscheinungen zu finden. Und besonders solche Dinge, die einfach in der Anschauung sich ergeben, wie die Ausdehnung und eine solche Unregelmäßigkeit in der Ausdehnung, wie sie uns beim Wasser, also bei einer Flüssigkeit entgegentritt, solche tatsächlichen Dinge wollen wir uns vor Augen stellen und innerhalb der Tatsachenwelt verbleiben. Das ist auf dem physikalischen Gebiet wirklicher Goetheanismus.
[ 19 ] Halten wir also dasjenige, was nun nicht eine Theorie ist, sondern was eine in der Außenwelt konstatierbare Tatsache ist, fest: Mit dem Übergang in den gasigen Zustand tritt eine Vereinheitlichung sämtlicher Substanzen auf der Erde ein. Und mit dem Übergang in den festen Zustand nach unten tritt ein Individualisieren, eine Differenzierung nach Individuen ein. Wenn wir uns nun fragen: Wie kann das eigentlich sein, was kann da zugrunde liegen, daß mit dem Übergang aus dem festen in den gasförmigen Zustand durch den flüssigen hindurch eine Vereinheitlichung eintritt, dann kommen wir aus unseren heute gangbaren Begriffen heraus überhaupt außerordentlich schwer zu einem Ausweg. Wir müssen da schon, um im Anschaulichen stehenbleiben zu können, anfangen, schwerwiegende Fragen zu stellen. Wir müssen zunächst fragen: Woher haben wir denn überhaupt die Möglichkeit, Körper zum Ausdehnen zu bringen und damit allmählich zur Vergasung und zu der charakterisierten Vereinheitlichung? Sie brauchen nur eine Umschau zu halten über all dasjenige, was Sie wissen können über die physikalischen Vorgänge der Erde, so werden Sie sich sagen müssen: Ohne daß Sonnenwirkung da wäre, könnten wir all diese Erscheinungen, die auch unter dem Einfluß des Wärmewesens stattfinden, auf der Erde überhaupt nicht haben. Sie müssen den Blick darauf wenden, welche ungeheure Bedeutung die Sonne in ihrem ganzen Wesen für die irdischen Erscheinungen hat. Und wenn Sie dies, was also wiederum in das Gebiet des Tatsächlichen gehört, ins Auge fassen, so werden Sie sich sagen müssen: Gerade jene Vereinheitlichung, die da auftritt bei dem Übergang von dem festen durch den flüssigen in den gasförmigen Zustand, sie könnte nicht eintreten, wenn die Erde nur sich selbst überlassen wäre. Wir können nur Anhaltspunkte gewinnen zu Vorstellungen über diese Sache, wenn wir über die irdischen Verhältnisse hinausgehen. Damit ist aber etwas außerordentlich Schwerwiegendes gesagt. Denn mit diesem Übergang des physikalischen Denkens durch die Denkweise der Accademia del Cimento und alles dessen, was damit zusammenhängt, wurden die alten Vorstellungen, die in Griechenland durchaus noch üblich waren, entkleidet alles Außerirdischen. Und Sie werden schon sehen, daß wir in den nächsten Tagen ohne historische Hilfe, rein aus der Sache heraus, zu demselben kommen werden. Aber ich werde vielleicht leichter zu Ihrem Verständnis den Zugang gewinnen, wenn ich diesen kleinen historischen Exkurs noch einschalte, den ich jetzt machen will.
[ 20 ] Ich sagte schon: Die eigentliche Bedeutung derjenigen Begriffe und Ideen, durch die man noch im alten Griechenland die physikalischen Erscheinungen hat begreifen wollen, ist verlorengegangen. Man hat begonnen zu experimentieren, und hat, ich möchte sagen, wortwörtlich, ohne den inneren Gedankenweg, der in Griechenland noch gemacht worden ist, die Vorstellungen, die Ideen aufgenommen. Dadurch vergaß die Menschheit gewissermaßen alles dasjenige, was mit diesen physikalischen Vorstellungen im alten Griechenland noch verbunden war. Das alte Griechenland hat noch nicht gesagt: fest, flüssig, gasförmig —, sondern dasjenige, was das alte Griechenland gesagt hat, können wir in unserer Sprache übersetzen damit, daß wir sagen:
Was fest war, bezeichnete das alte Griechenland mit Erde.
Was flüssig war, bezeichnete das alte Griechenland mit Wasser.
Was gasförmig war, bezeichnete das alte Griechenland mit Luft.
[ 21 ] Und es ist ganz unrichtig, zu glauben, daß, wenn wir unsere Wortbedeutungen Erde, Wasser, Luft haben, und dann irgendwo in älteren Schriften, die noch von der griechischen physikalischen Anschauung beeinflußt sind, die entsprechenden Worte wiederfinden, daß sie dann dasselbe bedeuten. Wir müßten, wenn wir irgendwo in alten Schriften den Ausdruck «Wasser» sehen, ihn übersetzen mit Flüssigkeit, wenn wir den Ausdruck «Erde» sehen, mit festen Körpern. Nur dadurch würden wir richtig die alten Schriften übersetzen. Aber darin liegt etwas sehr Bedeutsames. Dadurch, daß der feste Zustand — wie gesagt, wir wollen das in den nächsten Tagen aus der Sache selbst heraus finden, ich will heute nur durch diesen historischen Exkurs zu ihrem Verständnis den Zugang gewinnen -, dadurch, daß der feste Zustand mit Erde bezeichnet wurde, drückte man insbesondere aus, daß dieser feste Zustand allein gebunden ist an die Gesetzmäßigkeit unseres irdischen Planeten. Man bezeichnete das Feste deshalb als Erde, weil man dadurch ausdrücken wollte: Wenn ein Körper fest wird, so gerät er ganz und gar unter den Einfluß der irdischen Gesetzmäßigkeit. Wenn dagegen ein Körper Wasser wird, dann steht er nicht mehr bloß unter dem Einfluß der irdischen Gesetzmäßigkeit, sondern unter dem Einfluß des ganzen Planetensystems. Die Kräfte, die sich geltend machen in einem flüssigen Körper, in dem Wasser, die sind nicht bloß von der Erde herrührend, sondern von dem Planetensystem. Da wirken hinein die Kräfte von Merkur, Mars und so weiter in das, was flüssig ist. Aber sie wirken so, daß sie gewissermaßen von den Richtungen her, in denen diese Planeten stehen, eben wirken, und eine Art Resultierende in jeder Flüssigkeit werden.
[ 22 ] Man hatte also das Gefühl, indem man nur die festen Körper als Erde bezeichnete, daß nur diese unter dem Einfluß der irdischen Gesetzmäßigkeit stehen; daß, indem ein Körper schmilzt, er unter Gesetzmäßigkeiten gerät, die außerirdische sind. Und indem man gar die gasförmigen Körper Luft nannte, da hatte man — wie gesagt, ich stelle es Ihnen jetzt historisch dar — die Empfindung: Ein solcher Körper steht unter dem Einfluß des vereinheitlichenden Sonnenwesens. Er wird hinausgehoben aus dem Irdischen und aus dem bloß Planetarischen und steht unter dem Einfluß des vereinheitlichenden Sonnenwesens. Und man hatte von dem irdischen Luftwesen auch die Anschauung, daß an seiner Konfiguration, seiner inneren Beschaffenheit und Substantialität die Kräfte der Sonne im wesentlichen tätig sind. Die alte Physik hatte einen kosmischen Charakter. Die alte Physik war geneigt, mit Kräften, welche dem Gebiete des Tatsächlichen angehören, zu rechnen. Denn der Mond, der Merkur, der Mars und so weiter sind Tatsachen. Aber indem man verloren hatte die Quelle zu dieser Anschauung und zunächst nicht entwickeln konnte das Bedürfnis nach neuen Quellen, verlor man vollständig die Möglichkeit, andere Vorstellungen zu gewinnen als diese: Wie die festen Körper, selbst in ihrer Ausdehnungsfähigkeit, in ihrer ganzen Konfiguration und Gestaltung abhängig sind von der Erde, so auch die flüssigen und luftförmigen. Sie werden zwar sagen, es fällt keinem Physiker ein, abzusehen davon, daß die Sonne die Luft erwärmt und so weiter. Das tut er zwar nicht, aber, indem er dabei von Vorstellungen ausgeht, wie ich es gestern charakterisiert habe, indem er sich die Sonne in ihrer Erwärmefähigkeit nur nach dem Muster der aus dem Irdischen gewonnenen Begriffe vorstellt, verirdischt er die Sonne, statt das Terrestrische durch das Solare zu erklären.
[ 23 ] Das ist nun das Wesentliche, daß in der Zeit vom 15. bis 17. Jahrhundert vollständig verlorengegangen ist das Bewußtsein, daß unsere Erde ein Körper im ganzen Sonnensystem ist, daß dann auch jedes einzelne auf der Erde zu tun haben muß mit dem ganzen Sonnensystem und daß das Festwerden der Körper geradezu darauf beruht, daß sich gewissermaßen das Irdische emanzipiert von dem Kosmischen, daß es sich herausreißt, sich selbständige Gesetze gibt, während zum Beispiel das Gasförmige, die Luft, in seiner Gesetzmäßigkeit unter dem Einfluß des für die ganze Erde einheitlichen Sonnenwesens bleibt. Das ist es, was dann dazu geführt hat, daß man genötigt worden ist, für die Dinge, die früher aus dem Kosmischen erklärt worden sind, irdische Erklärungen zu finden. Da man abgesehen hat davon, die Kräfte zu suchen, die vom Planetensystem ausgehen müssen, wenn ein fester Körper, zum Beispiel Eis, flüssig wird, zu Wasser wird, indem man abgesehen hat, sie im Planetensystem zu suchen, mußte man sie hineinverlegen in das Innere des Körpers selber. Man mußte nachdenken, nachspintisieren darüber, wie ein solcher Körper aus Molekülen und Atomen zusammengesetzt ist. Und man mußte diesen unglückseligen Molekülen und Atomen die Fähigkeiten zuschreiben, die von innen heraus nun bewirken sollten, daß ein Festes in Flüssiges, ein Flüssiges in Gasförmiges übergeführt wird, die Fähigkeiten, die man früher hergeleitet hatte von dem, was tatsächlich im Raum gegeben war, aber allerdings im außerirdischen Kosmos. So muß man verstehen den Übergang der physikalischen Vorstellungen, wie er sich insbesondere gezeigt hat im krassen Materialismus aller Abhandlungen der Accademia del Cimento, die etwa zehn Jahre geblüht hat, von 1657 bis 1667. Man muß sich vorstellen, daß dieser krasse Materialismus dadurch entstanden ist, daß man allmählich verloren hat Ideen, die veranschaulichen den Anschluß unseres Irdischen an das Kosmische, das Außerirdische. Heute stehen wir vor der Notwendigkeit, hier wiederum Umkehr zu schaffen. Man wird aus dem Materialismus nicht herauskommen, wenn man sich nicht wiederum in die Lage versetzt, weniger philiströs zu sein gerade auf dem Gebiete der Physik. Das Philiströse liegt nämlich darin, daß man von konkreten zu abstrakten Begriffen übergeht, denn niemand liebt die abstrakten Begriffe mehr als der Philister. Er möchte alles mit ein paar Formeln, mit ein paar abstrakten Begriffen umfassen. Aber auch die Physik selber wird nicht weiterkommen, wenn sie fortspinnt in solchen Anschauungen - ich will nicht einmal bloß die Theorien anführen -, wie sie seit dem Materialismus der Accademia del Cimento gang und gäbe geworden sind. Vorwärts kommen wir dadurch, daß wir gerade in einem solchen Gebiet, wie der Wärmelehre, den Anschluß wiederum zu gewinnen versuchen an umfassendere, weiter ausgreifende Ideen, als sie die neuere materialistische Physik gehabt hat.
Second Lecture
[ 1 ] Yesterday we touched on the fact that under the influence of heat, what we call the body in everyday life expands. Today we will begin by looking at how so-called solid bodies expand under the influence of heat. For this purpose, we have clamped an iron rod here so that we can memorize the facts and then use them appropriately in our lessons — it is simple and elementary at first. We want to heat this iron rod and illustrate its expansion by means of the lever arm attached here, which will indicate the change in length. When I press here with my finger, this pointer moves upwards.

[ 2 ] You will see that when we heat this rod, this pointer will also move upward, which will prove to you that the rod is expanding. You can already see how the pointer is moving upward. And you can see that as the heating continues, the pointer moves further and further upward, which proves to you that the expansion increases with temperature. If I had used any other metal instead of the substance of this body and we then measured it precisely, we would obtain a different expansion. We would find that different bodies expand to different degrees. So we would first have to state that the capacity for expansion, the strength of the expansion, depends on the substance. We will initially disregard the fact that we actually have a cylinder in front of us. Let us first mentally image that we simply have a body of a certain length without thickness or width in front of us, and let us initially observe the expansion in only one dimension. If we illustrate this, we get the following:

[ 3 ] If a rod is held here and we consider it only as a length, we first want to designate the length of this rod as \(l_0\) for the temperature, the degree of heat, from which we start. And we then designate the length of the rod that it acquires when we first increase its temperature by 1 degree as \(l\). Now I said that the rods expand to different degrees depending on whether they are made of one substance or the other. We can now always express the degree of expansion, in this case from \(a\) to \(b\), as a fraction that represents the ratio of the expansion to the original length of the rod. Let's denote this proportional rate of expansion by \(\alpha\). Then we have the length of the rod after it has expanded, i.e., the length \(l\), which we can think of as being composed of its original length \(l_0\) and the piece that it has gained in length due to the expansion. We have to add this. By defining \(\alpha\) as a fraction that indicates the ratio between the expansion and the original length, by multiplying \(l_0\) by \(\alpha\), I get the tendency of the rod to expand, and because the expansion becomes more significant as the temperature rises, I have to multiply this by the temperature increase \(t\). So I can say: The rod length \(l\) after expansion
$$l = l_0 + l_0 \alpha t = l_0(1 + \alpha t)$$
[ 4 ] This means that if I want to determine the length of a rod that has expanded due to heating, I must multiply its original length by a factor given here by 1 plus the temperature multiplied by the relative expansion capacity of the substance in question. Physicists have become accustomed to calling \(\alpha\) the coefficient of expansion for the substance in question.

[ 5 ] Now I have considered a rod here. In reality, we do not have rods of no width and no height. In reality, we have three-dimensional bodies. If we now move from this length expansion back to the purely theoretical surface expansion, we can transform this formula in the following way: Let us assume that instead of the length extension as shown here, we now consider the surface extension. If we had a surface here, we would have to be aware that the surface extends in two dimensions, so that after heating it would have approximately this size. We would then have not only the length extension according to |, but also the width extension according to \(b\). And if we first consider the linear expansion, here \(l_0\), we would again have the expansion in this direction, which I have now specified, according to \(l\). And we have
$$l = l_0(1 + \alpha t). \qquad (1)$$
[ 6 ] Now let's also consider the width expansion \(b_0\), which has expanded to \(b\), so I would now have to write — it goes without saying that the expansion law remains the same —
$$b = b_0(1 + \alpha t) \qquad (2)$$
[ 7 ] Now you know that the area is obtained by multiplying the length by the width. So I get the entire area, which is the original one here, by multiplying \(b_0\) by \(l_0\), and here the area after expansion by multiplying \(l_0(1 + \alpha t)\) by \(b_0(1 + \alpha t)\).
$$lb = l_0(l + \alpha t)b_0(1 + \alpha t) \qquad (3)$$
That means I get:
$$lb = l_0b_0 (1 + \alpha t)^2 \qquad (4)$$
But written out in full, this means:
$$lb = l_0b_0 (1 + 2\alpha t + \alpha^2 t^t) \qquad (5)$$
[ 8 ] This would give me the formula for the expansion of an area.
[ 9 ] If you now add thickness to the area, I have to treat this thickness in the same way. I would then have to add d and get:
$$ lbd = l_0b_0d_0(1 + 3\alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3). \qquad (6)$$[ 10 ] And when you look at this formula, please pay particular attention to the following: If we look at the first two terms of this formula (6), you will find t at most in the first power. If you look at the third term, you will find t in the second power, and the last t in the third power. I ask you to pay particular attention to these last two terms of the formula for expansion. Note that when we have the expansion of a three-dimensional body, we get a formula expression for it that contains the third power of the temperature — I want to disregard the second power of the temperature. It is extremely important to note that we get the third power of the temperature here.
[ 11 ] Since I must always take into account that we are here at the Waldorf School and that everything must be oriented toward education, it is necessary to point out to you that if you study the same derivation that I have made here in the standard physics textbooks, you will find a considerable difference between the way I have presented the matter here and the description in the standard physics textbooks. I will now tell you how the matter is presented in the standard physics textbooks. It says: " is a ratio—it is usually a fraction. The expansion is very small in relation to the original length of the rod. If I have a fraction with a larger number in the denominator than in the numerator, then when I square or cube it, I get a much smaller number. If I square a third, I get a ninth, and if I cube a third, I get a twenty-seventh. This means that the third power is already a very, very small fraction. "& is a fraction that usually has a very large denominator. That is why the standard physics textbooks say: If I now form the square, \(\alpha^2\) or even \(\alpha^3\), which I have to multiply by \(t^3\), these are very small fractions that can simply be omitted. So the standard physics textbooks say: We simply omit these last terms of the expansion formula and write \(l \cdot b \cdot d\) — this is the volume that an expanding body assumes at a certain temperature, so I will write \(V\) -:
$$V = V_0(1 + 3 \alpha t). \qquad (7)$$
[ 12 ] In this way, the formula is written for the expansion of a solid body, simply by referring to the fact that the fraction \(\alpha\) squared and, in particular, cubed gives such small numbers that they can be omitted. You know, this is how it is presented in standard physics textbooks. Well, this omits the most important thing that matters if one really wants to study thermodynamics properly. This will become clear to us as we proceed.

[ 13 ] Not only solids expand due to heat, but liquids do as well. Here you have a colored liquid so that you can see it. We will heat this colored liquid (see drawing). You will now see that after a while the colored liquid column rises, and from this you will conclude that liquids expand in the same way as solid bodies. You see, the colored liquid rises, so the liquid expands when heated.
[ 14 ] Now, we can also examine the expansion of an air-like body. To do this, we have air here in the flask, which simply enters from the outside (see drawing on page 36). We now seal the air in the flask and heat it. We have a communicating vessel here. The property of communicating vessels is that the level of the liquid in them is the same on both sides, i.e., it covers both sight glasses. You will now see what happens when we simply heat the air inside, i.e., an air-like body. We will achieve this by placing heated water at a temperature of 40°C in the vessel (see drawing on page 36). You can see that the mercury column on the right is already rising. Why is it rising? Because the gaseous body in this flask is expanding. The air flows out here, pressing on this mercury (left), while on the other side, the mercury column is lifted by the pressure, and you can see from this that this gaseous body has expanded. So we can say that solid, liquid, and gaseous bodies expand under the influence of the heat phenomenon, which is still unknown to us.

[ 15 ] But now, as we move on from the study of expansion in solid bodies, through the study of expansion in liquids, to the study of expansion in gaseous bodies, we encounter something very significant. I said earlier that the " here, the ratio of expansion to the original length of the rod, is different for different substances. If we were to examine the \(\alpha\) for different liquids, which would require further experiments that we cannot carry out here, we would still obtain different values for different liquid substances. However, if we examine \(\alpha\) for gaseous bodies, namely for gases, we see the peculiarity that \(\alpha\) is no longer different for different gaseous bodies, but that \(\alpha\), the coefficient of expansion, as it is called, is the same for the different gases, namely approximately \(\frac{1}{273}\). This fact is of great importance. We can see from this that, as we move from solid bodies to gaseous bodies, new conditions actually arise under the influence of heat. We see from this that the various gases do not behave according to their different substantiality, but that they behave toward heat simply according to their property of being gases, that becoming a gas is something that can, in a sense, come about as a common property of all bodies. Yes, we see from this that becoming a gas is something that unites all gases that we can know in the earthly sphere, at least in relation to this property of their expandability. Keep in mind that we simply come to the conclusion, based on expandability through heat, that as we move from solid bodies toward gases, the differentiated expansibility that we find in solid bodies is transformed into a kind of unity, into a uniform expansibility in gases, that is, that in our earthly realm, a differentiation of physicalities, if I may express myself cautiously, is linked to the solid state. I could also say that becoming solid is linked to an individualization of physicality. Very little attention is paid to this circumstance in modern physics. It is not pointed out because the most important things are simply concealed by eliminating certain variables that cannot be properly dealt with.
[ 16 ] One can only gain a deeper insight into what this is all about by calling on the history of physical development for a little help. All the mental images that prevail today in physics textbooks and in the treatment of physics in general are, after all, not yet very old. They essentially date back to the 17th century, and their fundamental character was shaped by everything that took place in the 17th century as part of the revival of a certain scientific spirit in Europe through the Accademia del Cimento in Florence, which was founded in 1657 and where an extraordinary number of experiments were carried out in a wide variety of fields, but particularly in the fields of heat, acoustics, sound, and so on. Just how young our common mental images are in this field becomes apparent when we take a closer look at certain specific events at the Accademia del Cimento. For example, it was there that the foundations for our modern thermometry were first laid. It was first noticed how, in a glass tube closed at the bottom with a cylinder, as you can see on every thermometer, the heating affects the mercury with which the glass tube is filled. For example, it was first noticed that there is an apparent contradiction between the view that had otherwise been gained, for example through an experiment in which a liquid simply expands, and what was particularly evident when an experiment was carried out that was intended to be instructive. The general view had been that liquids also expand. But when the experiment was carried out with mercury, it first fell under the heat and only then rose. An explanation for this had to be found in the 17th century, which was easy to do by saying: When I heat something, I first heat the outer glass. This expands. The space filled by the mercury becomes larger; it sinks at first, and the inner body only begins to rise slightly when the heat has penetrated to the inside. Such concepts only emerged in the 17th century. But in the 17th century, people were also very far behind in terms of all the ideas that were supposed to help them understand physics, because until that time, the actual Renaissance, Europe had paid so little attention to scientific concepts of this kind. It was a time when Christianity had to spread, which in a certain way prevented concepts from becoming established and developing in relation to physical phenomena. Then, when the Renaissance came and people became familiar with the mental images that already existed in ancient Greece, they found themselves in the following situation: on the one hand, encouraged by all kinds of willing support, institutes such as the Accademia del Cimento were formed, and there it was now possible to experiment. It was possible to demonstrate directly how physical phenomena occur. On the other hand, however, people were weaned off forming concepts about things. They were weaned off really thinking about phenomena. They took up the old Greek mental images again, which were now widely accepted, but they no longer understood them. And so they also took up the mental image of fire or heat without being able to understand in any way what was meant by this concept in ancient Greece. And now a deep gulf formed between thinking and what could be given to perception through experimentation. This gulf widened more and more, especially since the 17th century. The art of experimentation was then perfected, especially in the 19th century, but clear, distinct concepts did not accompany this perfection of the art of experimentation. And today, lacking such clear, distinct, visual concepts, we are often at a loss in the face of those phenomena that thoughtless experimentation has produced over time and which can only be fruitfully incorporated into human intellectual development if we find a way not only to experiment and observe the course of the experiment externally, but to truly enter into the inner workings of natural events.
[ 17 ] You see, when we penetrate into the inner workings of natural phenomena, something so extraordinary comes into consideration that completely new conditions arise in relation to expandability when we ascend from solid bodies to gases. But without expanding our entire physical imagination, we will never be able to truly comprehend such things, which are actually already present in reality today. In addition to these facts, which we have already mentioned, there is another that is extremely significant.
[ 18 ] Is it not true that, as a general rule, we can form the following statement from what we have already presented here: When we heat bodies, they expand; when they cool down again, they contract. So that the general statement could be formed: Bodies expand when heated and contract when cooled. However, you know from elementary physics that there are exceptions to this statement, above all a cardinal exception concerning water itself. When water is expanded and then contracted again, the strange thing is that if water has a temperature of 8° and then cools down, it contracts. That is only natural, I would say. But if you continue to cool it, it does not contract, but expands again. So ice, which is formed from water—we will talk about this formation later—can float on water because it is more expansive and therefore less dense than water. It is a peculiar phenomenon that ice can float on water! It stems from the fact that this general law of expansion and contraction exhibits an irregularity in the case of water, in that water does not generally follow this law without further ado. It would indeed be peculiar to our entire natural order if this were not the case, if this exception did not exist. If you observe a basin, a pond, and so on, you will see that even in severe winter there is only a layer of ice and the water does not freeze to the bottom. The reason why the water at the bottom remains unfrozen is that the ice that forms at the top floats and thus forms a cover, which protects the water below from further cooling. You always have a layer of ice on top and protected water below. This irregularity that occurs here is therefore related to something that actually—if I may use the somewhat bourgeois expression—has a great deal to do with the balance of nature. Now, you see, the physical approach we want to take here must be exactly as I indicated in the last course. We must avoid coming to the Achilles and the tortoise conclusion. We must avoid disregarding the obvious; we must make every effort to remain with the obvious, that is, with what can be observed. Therefore, we will always stick strictly to the obvious and try to find an explanation for the phenomena from the obvious. And especially those things that simply arise in perception, such as extension and such irregularities in extension as we encounter in water, that is, in a liquid, we want to keep such actual things in mind and remain within the world of facts. That is true Goetheanism in the field of physics.
[ 19 ] So let us hold fast to what is not a theory, but a fact that can be observed in the external world: with the transition to the gaseous state, a unification of all substances on earth occurs. And with the transition to the solid state, an individualization, a differentiation according to individuals, occurs. If we now ask ourselves: How can this actually be, what could be the basis for the fact that with the transition from the solid to the gaseous state through the liquid state, a unification occurs, then it is extremely difficult for us to find a way out of our current concepts. In order to remain within the realm of the concrete, we must begin to ask serious questions. We must first ask: Where do we even get the possibility of causing bodies to expand and thus gradually gasify and undergo the characterized unification? You need only look around at everything you know about the physical processes of the earth, and you will have to say to yourself: without the influence of the sun, we could not have any of these phenomena on earth that also take place under the influence of heat. You must turn your gaze to the enormous significance of the sun in its entire being for earthly phenomena. And when you consider this, which again belongs to the realm of reality, you will have to say to yourself: precisely that unification that occurs in the transition from the solid to the liquid to the gaseous state could not occur if the earth were left to its own devices. We can only gain clues to mental images about this matter if we go beyond earthly conditions. But this is an extremely serious statement. For with this transition of physical thinking through the thinking of the Accademia del Cimento and everything connected with it, the old mental images, which were still quite common in Greece, were stripped of everything extraterrestrial. And you will see that in the next few days, without historical assistance, purely from the matter itself, we will come to the same conclusion. But I will perhaps gain easier access to your understanding if I insert this little historical digression, which I now wish to make.
[ 20 ] I have already said that the actual meaning of those concepts and ideas through which people in ancient Greece sought to understand physical phenomena has been lost. People began to experiment and, I would say, literally adopted the mental images and ideas without the inner thought process that was still carried out in Greece. As a result, humanity forgot, in a sense, everything that was still connected with these physical mental images in ancient Greece. Ancient Greece did not yet say: solid, liquid, gaseous — but what ancient Greece said can be translated into our language by saying:
What was solid, ancient Greece called earth.
What was liquid, ancient Greece called water.
What was gaseous, ancient Greece called air.
[ 21 ] And it is quite incorrect to believe that when we have our meanings of earth, water, and air, and then find the corresponding words somewhere in older writings that are still influenced by the Greek view of physics, that they mean the same thing. When we see the term “water” somewhere in ancient writings, we would have to translate it as “liquid,” and when we see the term “earth,” we would have to translate it as “solid bodies.” Only in this way would we be translating the ancient writings correctly. But there is something very significant in this. By designating the solid state as earth — as I said, we will explore this further in the coming days, but today I only want to gain an understanding of it through this historical digression — by designating the solid state as earth, one expressed in particular that this solid state alone is bound to the laws of our earthly planet. One designated the solid as earth because one wanted to express that When a body becomes solid, it comes entirely under the influence of earthly laws. When, on the other hand, a body becomes water, it is no longer under the influence of earthly laws alone, but under the influence of the entire planetary system. The forces that exert themselves in a liquid body, in water, do not originate solely from the earth, but from the planetary system. The forces of Mercury, Mars, and so on, act on what is liquid. But they act in such a way that they exert themselves, so to speak, from the directions in which these planets are located, and become a kind of resultant in every liquid.
[ 22 ] So, by referring to only solid bodies as earth, one had the feeling that only these were subject to earthly laws; that when a body melts, it becomes subject to laws that are extraterrestrial. And by calling gaseous bodies air, one had — as I said, I am now presenting this to you historically — the feeling that such a body is under the influence of the unifying sun being. It is lifted out of the earthly and the merely planetary and is under the influence of the unifying sun being. And people also had the view of the earthly air being that the forces of the sun are essentially active in its configuration, its inner nature, and its substantiality. Ancient physics had a cosmic character. Ancient physics was inclined to reckon with forces that belong to the realm of the actual. For the moon, Mercury, Mars, and so on are facts. But by losing the source of this view and initially being unable to develop the need for new sources, one completely lost the possibility of gaining any other mental images than these: just as solid bodies, even in their expandability, in their entire configuration and form, are dependent on the earth, so too are liquid and gaseous bodies. You will say, of course, that no physicist would think of disregarding the fact that the sun warms the air and so on. He does not do so, but by starting from mental images such as I characterized yesterday, by imagining the sun in its capacity to warm only according to the pattern of concepts derived from the earthly, he earthbound the sun instead of explaining the terrestrial through the solar.
[ 23 ] The essential point is that between the 15th and 17th centuries, the awareness that our Earth is a body in the entire solar system was completely lost, that everything on Earth must therefore have something to do with the entire solar system, and that the solidification of bodies is based precisely on the fact that the earthly emancipates itself, as it were, from the cosmic, that it breaks away and gives itself independent laws, while, for example, the gaseous, the air, remains in its lawfulness under the influence of the solar being that is uniform for the entire Earth. This is what then led to the necessity of finding earthly explanations for things that had previously been explained from the cosmic perspective. Since people refrained from seeking the forces that must emanate from the planetary system when a solid body, for example ice, becomes liquid, becomes water, by refraining from seeking them in the planetary system, they had to transfer them into the interior of the body itself. They had to think about it, speculate about how such a body is composed of molecules and atoms. And one had to attribute to these unfortunate molecules and atoms the abilities that were now supposed to cause, from within, a solid to be transformed into a liquid, a liquid into a gas, abilities that had previously been derived from what actually existed in space, but in the extraterrestrial cosmos. This is how one must understand the transition in physical mental images, as it was particularly evident in the crass materialism of all the treatises of the Accademia del Cimento, which flourished for about ten years, from 1657 to 1667. One must have the mental image that this crass materialism arose from the gradual loss of ideas that illustrate the connection between our earthly existence and the cosmic, the extraterrestrial. Today, we are faced with the necessity of reversing this trend. We will not escape materialism unless we put ourselves in a position to be less philistine, especially in the field of physics. Philistinism lies in the transition from concrete to abstract concepts, for no one loves abstract concepts more than the philistine. He wants to encompass everything with a few formulas, with a few abstract concepts. But physics itself will not make any progress if it continues to spin such views—I don't even want to mention the theories—as have become commonplace since the materialism of the Accademia del Cimento. We can make progress by trying to reconnect with more comprehensive, far-reaching ideas than those of modern materialistic physics, especially in a field such as thermodynamics.

