The Fourth Dimension
GA 324a
Questions and Answers XXI
12 April 1922, The Hague
Question about higher-dimensional space.
We can say that the ordinary axial coordinate system describes three-dimensional space. Schematically speaking, we can proceed on the basis of certain algebraic assumptions and, on an abstract level, repeat the process that led us from a plane to three-dimensional space. The result is four-, five-, or \(n\)-dimensional space. We can even construct figures such as Hinton's tessaract. The tessaract, however, is not a real figure but simply the projection of a true tessaract into three-dimensional space. [Note 145]
On a purely theoretical and abstract level, there is nothing wrong with such deductions. On a theoretical level, we also can move from three-dimensional space to the fourth dimension in time simply by using the formulas and calculations and taking into account the leap that we are making, because moving into time is different from moving from the first to the second to the third dimension. By refining this process, however, we can indeed make the transition to time. The result is an abstract four-dimensional space. We can remain on the abstract, purely intellectual level as long as we do not need to visualize what we are doing. When we attempt to do so, however, we are confronted with a problem of elasticity, whereas our purely abstract train of thoughts led to a regressus in infinitum. We also can imagine initially that a pendulum simply will continue to swing indefinitely, but in dynamics we have oscillations. That is the reality of the situation.
When we rise to the level of imaginative perception, we cannot simply repeat the process indefinitely, assuming the existence of a fourth and subsequent dimensions. If we use the notation \(+ a\) for the first dimension, \(+ b\) for the second, and \(+ c\) for the third, we cannot, if we are describing real space, write the fourth dimension as \(+ d\). Instead, the reality of the situation forces us to write \(- c\). The fourth dimension simply nullifies the third, and only two remain. At the end of the process, therefore, we are left with two dimensions instead of four. Similarly, if we assume the existence of a fifth dimension, we must use the notation \(- b\) for it and \(- a\) for the sixth. That is, we come back to a point. [Note 146] Through the principle of elasticity, we have returned to the starting point. This phenomenon not only is present in Imagination—that is, as a subjective experiment—but also becomes a reality in the way I described the day before yesterday. [Note 147]
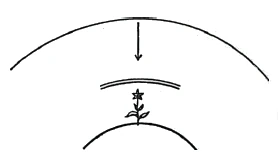
As long as we are looking at the Earth's surface here and plant roots here (Figure 66a), we are dealing with a specific manifestation of gravity and remain within the ordinary dimensions of space. When we attempt to explain the shape of a flower, however, these ordinary dimensions no longer suffice. Instead of taking the intersection of the axes as our starting point, we must begin with infinite space, which is simply the counterpart of the point. Instead of moving centrifugally outward, we must move centripetally inward (Figure 66a). The result is a wavy surface. Instead of dissipating into the distance, pressure is exerted from outside, resulting in gliding and scraping movements. Such movements, which result from pressure, cannot be described correctly by taking the intersection of axes as the starting point for our coordinates. Instead, we must take an infinitely large sphere as the center of the coordinates, and the coordinates must all move toward the center. [Note 148] That is, as soon as we move into the etheric realm, we need to apply an axial coordinate system that is the opposite—also qualitatively speaking—of the ordinary coordinate system. Ordinary theories about the ether of physics err in not taking this difference into account, making it difficult to define the ether. It is sometimes seen as a fluid and sometimes as a gas. It is wrong to apply a coordinate system that radiates from a central point to the ether. As soon as we enter the ether, we must take a sphere and construct the whole system from the outside in, instead of the other way around.

Such issues become interesting when they are traced mathematically and enter the domain of physics. Developing our theories, which begin to seem very realistic, would contribute a great deal to solving problems of limits. At present, however, such theories meet with very little understanding. For example, I once attempted to introduce this subject in a lecture to the mathematical society of a university. [Note 149] In this lecture, I said that if these are the asymptotes of a hyperbola and these its branches, we must imagine that the part on the right is dissipating, while the part on the left is becoming concentrated. That is, a complete reversal takes place (Figure 66b). Such considerations gradually lead us to a more concrete treatment of space, but this treatment finds little acceptance. Purely analytical mathematicians often are somewhat biased against synthetic geometry. Modern synthetic geometry, however, permits us to move away from purely formal mathematics and tackle empirical problems. As long as we apply only purely analytical geometry, we cannot approach the domain of reality. Analytical geometry allows us to establish only the endpoints of coordinates, their geometric locations, and so on. When we restrict our constructions to lines and circles, we need the help of images and are forced to turn to visualization for help. What makes synthetic geometry so beneficial is that it allows us to leave behind the formal aspect of mathematics. It shows us how we must conceive of the mathematical element in nature. [Note 150]
Question about the theory of relativity.
The discussion about the theory of relativity is endless. [Note 151] This theory cannot be refuted from our vantage point as observers of cosmic events in three-dimensional space. That is, it is impossible to refute the theory of relativity on the basis of perceived space. As far as our perception is concerned, of course, it makes no difference whether a sphere flattens out or space as a whole expands inward in the direction of the sphere's flattening. Thus, as long as we are dealing with the perspective of three-dimensional space, Einstein's theory of relativity is absolutely correct. This theory appeared at the very moment in humanity's evolution and in the history of science when we first managed to think in purely spatial terms—that is, to take Euclidean space as our starting point for further thinking, whether in the sense of non-Euclidean spaces or in the sense of relativity theory. It is impossible to refute Einstein's theory in three-dimensional space.
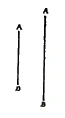
We can begin to discuss the possibility of refuting this theory only when we discover how to make the transition to the etheric realm—that is, the transition from the three-dimensional spatial body to the ether body. The ether body is centripetally, rather than centrifugally, formed. In your ether body, you dwell within the totality of space. For example, your inner perception of the distance between point A and point B is sometimes this and sometimes that (Figure 67a). Having recognized this phenomenon, you can say that one or the other of the points must have moved, in absolute terms, but to do that you yourself must stand within the totality of space. At this point, discussion becomes possible. For this reason, I am convinced that all of our discussions of current concepts about the theory of relativity must end in the question, "Well, how do you know that?" In contrast, as soon as we make the transition to inner perception—a domain where absolutes can be discovered—we are forced to realize that issues such as the theory of relativity show us that we have arrived at what Nietzsche calls the observers standpoint, of which the theory of relativity represents the most extreme version. For anyone who accepts this standpoint, the theory of relativity is simply a fact, and no arguments against it are possible. It can, however, be eliminated from practical considerations. A fanatical relativity theorist in Stuttgart once explained why it makes no difference whether we make a movement in one direction or the opposite direction. If I hold a matchbox in one hand and a match in the other, the result is the same whether I move the match past the box or the box past the match. Of course, in such cases the theory of relativity is absolutely correct, but I would have liked to shout out, "Please try again with the box nailed to the wall!"
This in no way diminishes the validity of the theory of relativity. It simply shows that just as we can move from two-dimensional space into the dimension of depth, we can move into the spiritual element from any location in the world. Then and only then does the theory of relativity cease to be valid. That's why I said that discussions about the theory of relativity tend to go on ad infinitum, because it is irrefutable from the observer's standpoint. Any arguments against the theory can always be disputed.
As an observer, you stand outside what you are observing; you must make a radical distinction between subject and object. As soon as you rise to higher levels of knowledge, subjectivity and objectivity cease. There is much more that could be said on this subject than can possibly be said in the context of a question-and- answer session, but I would like to submit one more idea as a stimulus to further thinking. As long as we remain in the beholder's world, in the world of space, relativity theory as such is irrefutable. On first escaping from this world, we enter worlds where we are not mere beholders but share the experience of the object, such as pain, for example. As soon as you learn to shift from mere relationships with other beings—and it is understandable enough that a theory of relativity is possible only within relationships—to the pain of shared inner experience, to use an example, it is no longer possible to speculate about whether this experience is relative. Thus, you cannot construct contradictions and then say that because a contradiction exists, the situation is not real. In life, contradictions are reality, because the beings that constitute life belong to different but intersecting spheres. As soon as you make the transition to reality, it is no longer permissible to say that any contradiction that exists must be resolved. If it is real, it cannot be resolved. My point here is that the theory of relativity is a natural development in the world of relationships. No arguments could be raised against this theory if the beholder's standpoint were the only possible perspective. As soon as we become involved in beings, however, and in pain and pleasure, the theory of relativity is no longer tenable.
QUESTION: Dr. Steiner, what do you mean when you say that the physical body is a spatial body while the body of formative forces is a temporal body? The physical body is also active in time when it grows and declines.
Yes, but your statement is based on imprecise thinking, if I may say so. To give it a more exact foundation, you first would have to analyze the concept of time. Consider this: In the reality we usually encounter, space and time intermingle. We can conceive of the physical body as spatial and the body of formative forces as temporal only when we separate space and time. In our usual objective knowledge, time is not present as a given. As you know, time is measured in terms of space,—that is, changes in spatial units are our means of knowing about what we call time. But now imagine a different way of measuring time. You no longer measure time in terms of space when you shift to a true experience of time, which people usually do unconsciously. Our thinking actually becomes conscious through imaginative cognition.
You have a true experience of time, for example, if you examine your soul life on April 12, 1922, at 4:04 and however many seconds. You see a temporal cross-section of your soul life. Although you cannot say that this temporal section contains any particular spatial section, it includes all of your immediate earthly past. If you want to draw it schematically, and the stream of your experience flows from a to \(b\), you must draw the section \(AB\) (Figure 67b). 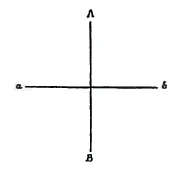
It is important to be able to see this time body as an organism. As you know, when you have a digestive disturbance, for example, you may find that other parts of your spatial organism also are affected adversely. In the spatial organism, individual areas are spatially separate from each other, while in our time organism—in spite of the fact that we differentiate between later and earlier—different times are related organically. I sometimes use the following example. When some very old people talk to younger ones, especially to children, their words seem to bounce right off; they mean nothing to the children. This is not the case with other old people. When they talk to children, their words seem to flow straight into the children's souls. To find the origin of the power of old people to bless others, you sometimes have to go back to their early childhood. (We usually do not study matters such as this, because we very seldom look at the whole person. We do not focus our attention long enough to observe such things. The scope of our present powers of observation is inadequate. That is a task for anthroposophy.) If you go back far enough, you will find that those who possess an unusual spiritual power to bless others in their old age, whose words flow as blessings into young people, learned how to pray in their own childhood. Metaphorically speaking, we can say that the folded hands of childhood become the blessing hands of old age. [Note 152]
Here you see a connection between a person's influence on others in old age and the pious sentiments and so on that were present in that person's early childhood. Earlier qualities and later ones are connected organically. There are an infinite number of such connections in each person, but we see them only when we understand the whole human being. Today our whole life is external to this reality. We think we are steeped in reality, but we deceive ourselves. In today's culture, we are abstractionists. We pay no attention to true reality and therefore disregard qualities such as those I mentioned. We also pay no attention to the fact that when we teach children, especially in the elementary grades, we must avoid giving them sharply defined concepts. The effect of such concepts on later life is similar to that of binding limbs and not allowing them to grow larger. What we communicate to children must be an organism, and it must be flexible. I hope that you are gradually becoming able to see what I mean by an organism. Of course, Imagination alone makes it possible to grasp this meaning completely. Nonetheless, it is possible to gain an idea of the nature of an organism simply by realizing that the temporal course of events in the life of a human being is related to the time organism rather than to the space organism.
You see, time possesses an inherent reality, as you can infer from mathematics. I believe it was Ostwald—in any case, it was not an anthroposophist but simply someone who is not a materialist—who pointed out in a wonderful discussion of this subject that, unlike mechanical processes, organic processes that take place over time are not reversible. [Note 153] In fact, ordinary calculations always remain external to temporal processes and do not allow us to approach them. For example, if you insert negative numbers into a formula for calculating eclipses of the Moon, you get instances in the more distant past, but you do not move away with the things. You move only in the sphere of space. Thus, we develop a correct idea of the actual physical human body only when we are able to separate the temporal element from the spatial. This is fundamentally important with regard to human beings, because we cannot come to any understanding of human beings if we do not know that the temporal element in humans runs its course as an independent entity and that the spatial element is governed by the temporal or dynamic element. In machines, however, the temporal element is only a function of activity in space. That is the difference. In humans, the temporal element is a real entity, while in mechanical devices the temporal element is only a function of space.
QUESTION: Einstein says that the time-space continuum is four-dimensional. If I understood correctly, you said that the fourth dimension becomes two dimensional because the fourth dimension is a negative third dimension. Should this be interpreted to mean that there is a connection between the imaginative world and Einsteins continuum? According to conventional scientific thinking, I would have to conclude that such a space is a plane. Consequently, the imaginative world would be a very specific plane in three-dimensional space. It would not have to be straight, and it would not have to remain in the same place, but it would have to be possible to confirm its presence at any given moment. My thoughts on this subject are probably not in line with anthroposophy, but I would like to know what anthroposophy has to say about it.
With the exception of a few comments, your thoughts are quite in line with anthroposophy. I would like to add that it is absolutely correct that when we attempt to shift from the three dimensions to the fourth on a real rather than abstract level, we must use a negative sign to describe the fourth dimension. That is, the transition to the fourth dimension simply eliminates or cancels out the third, just as debt cancels out savings. There is no other way of imagining the situation. But if we simply hurry on abstractly, we come to the regressus in infinitum that assumes the existence of more and more dimensions. This, however, is an abstract way of continuing and is not based on actually looking at the situation. When we enter the imaginative world, we do indeed confront a plane world, to use an expression borrowed from geometry. We confront the world of the plane of time. One peculiar feature of this world is that it can no longer be referred back to the third dimension of space. This is difficult to understand, but you will find an analogous situation in synthetic geometry, which is forced to consider the boundary of three-dimensionality—if, in fact, we impose boundaries on the three-dimensional world—as a surface and as a plane surface rather than a spherical surface. That is, synthetic geometry assumes that three-dimensional space is bounded by a plane. When you reach the boundary of three-dimensionality, you find a plane whose limit, in turn, must be imagined as a straight line rather than a circle, and this straight line has one, rather than two, endpoints. [Note 154] At this juncture, your thinking and your perception cannot completely coincide, no matter how consistent it is to speak of a plane as the boundary of three-dimensional space, of a straight line as the boundary of a plane, and of a single infinitely distant point as the limit of a straight line. To synthetic geometry, these ideas are real. Synthetic geometry plays into the perception that develops in the imaginative world. But when we say that the imaginative world lies in a plane, we cannot refer this plane back to three-dimensional space by defining its coordinates. It is lifted out of three-dimensional space and is anywhere and everywhere. This is difficult to imagine because we are used to visualizing in three-dimensional space. The imaginative world, however, does not lie in three-dimensional space, and the definitions of three-dimensionality do not apply to it.
We find another analogue for the imaginative world in art, when we practice painting on the basis of color. When we do so, we are working on a flat surface, or, if we work on a curved surface, its curve does not originate in the painting but in other circumstances. When we paint on a plane, our possibilities are not limited to drawn perspective, which is a relatively recent discovery, as you may know. Perspective appeared very late in the history of painting, only a few centuries ago. [Note 155] In addition to drawn perspective, however, we can utilize the perspective inherent in color. [Note 156] We have been using such principles in our painting in Dornach. On the basis of feeling and color, rather than thoughts, yellow appears to come toward us so strongly that it is almost aggressive. In contrast, when we use blue paint, the color recedes, yet both colors lie on the same surface. Thus, it is possible to express three-dimensional phenomena even though only a two-dimensional expanse is available to us. This is simply an example to help you visualize the situation, because the imaginative world is not the same as the world of painting.
Although the ideas you expressed in your question are very true to anthroposophy, we cannot really say without qualification that the imaginative world has a connection to Einstein's continuum. Einstein's continuum is based on abstraction rather than perception. Its fourth dimension is constructed as an analogue to the other three dimensions, which is not acceptable when we move from objective cognition in space to real suprasensible cognition, which manifests first as Imagination and can be expressed in spatial terms only by allowing the third dimension to be cancelled out by its negative. What I am going to say next will seem very daring to some,—nonetheless, it is my experience. In reality, the situation looks like this: When you function in the objective world with healthy common sense, your orientation is derived only from the three dimensions of space. The first dimension is inherent in your own upright posture, the second in your left-right dimension, and the third in the focusing of your eyes. You do not dwell in these three dimensions when you are in the imaginative world. There, you dwell only in two dimensions. If I had to locate these dimensions in space, I would have to take a vertical section through the human being. In Imagination, we can speak only of the dimensions of up and down and right and left. When you move in the imaginative world, these are the only dimensions you carry with you. For this reason I cannot say that they relate to a coordinate system in space. I cannot define them in terms of Euclidean geometry. To our perception, however, they are real. It makes no sense to talk about three dimensions in the context of the imaginative world. We must realize that we are dealing with an experience of two-dimensionality, an experience we cannot have in the objective world. Two dimensions are a reality in the imaginative world, and a single dimension is a reality in the inspired world. All Inspirations move vertically, if indeed we want to assign them a location in space. Intuition is point-like, but it to cannot be referred to a coordinate system. In these higher realms, we cannot revert to Euclidean space.
For more information on Hinton, see Note 1 to the lecture of March 31, 1905. On the tessaract, see the lecture of May 31, 1905, and the relevant notes.
See Notes 10 and 11 and the corresponding passages in the question-and-answer session of April 7, 1921.
See Rudolf Steiner's lectures of April 8, 9, and 10, 1922
See the similar passages at the end of Rudolf Steiners lecture of January 10, 1921 (GA 323, pp. 199-200) and at the beginning of the lecture of January 18, 1921 (GA 323, pp. 318-320).
Presumably Rudolf Steiner refers here to the lecture he gave to the Mathematical Society in Basel during the winter semester of 1920-1921. For more about this lecture, see the essay Über einen mathematischen Vortrag Rudolf Steiners in Basel ("On a Mathematical Lecture by Rudolf Steiner in Basel") in Beiträge zur Rudolf Steiner Gesamtausgabe ("Articles on Rudolf Steiner's Complete Works"), no. 114/115, Dornach, 1995.
See the parallel passages in the lectures of January 11, 1921 (published in Gegenwart ['The Present"], vol. 14, pp. 49-67, especially p. 65) and April 5, 1921 (GA 76).
See the question-and-answer session of March 7, 1920, and the relevant notes.
For more on this subject, see the lectures of October 28, 1909, and February 10, 1910, in Rudolf Steiner's Metamorphosen des Seelenlebens ('The Metamorphoses of Soul Life") and Pfade der Seelenerlebnisse ("The Paths of Soul Experience"), GA 58 and 59.
Friedrich Wilhelm Ostwald (1853–1932), chemist, color theorist, and scientific philosopher. In his lecture Die Überwindung des wissenschaftlichen Materialismus ("Overcoming Scientific Materialism) of September 20, 1895, which included a plea for his own energetics-based worldview and consciously contrasted it to the mechanistic worldview of Emil du Bois-Reymond (1818–1896), Ostwald said:
While efforts to interpret the familiar phenomena of physics in mechanical terms may seem in vain, having ultimately failed in every single serious attempt, the conclusion is unavoidable that success is even less likely with regard to the incomparably more complex phenomena of organic life. The same principled contradictions apply here, too, and the claim that all natural phenomena essentially can be traced back to mechanical phenomena cannot even be considered a usable working hypothesis,- it is a simple error. This error becomes most apparent when we confront the following fact. A feature of all mechanical equations is that they permit changing the sign of the unit of time. That is, theoretically perfect mechanical processes can run backward as well as forward. In a purely mechanical world, therefore, there would be no earlier and later as we know them in our world. A tree could revert to the seed stage, a butterfly could be transformed back into a caterpillar, and an elderly person into an adult. The mechanistic worldview cannot explain why this does not occur, and because of the above-mentioned feature of mechanical equations, no such explanation is possible. Thus, the non-reversibility of true natural phenomena proves the existence of processes that cannot be described by mechanical equations and pronounces judgment on scientific materialism ([1895], p. 20).
Steiner means that a projective straight line must be visualized as having only one (rather than two) infinitely distant points.
The founder of modern perspective was Filippo Brunelleschi (1377–1446), the architect and builder of the cupola of the cathedral in Florence. The new theory of perspective was first promoted by the architect and scholar Leon Battista Alberti (1401–1472) and the painter and mathematician Piero della Francesca (1416–1492). A work by Albrecht Dürer (1471–1528), Underweysung der messung mit dan zirckel und richtscheyt in linien, ebnen, und gantzen corporen ("Instruction in Measuring with Compass and Straightedge in Lines, Planes, and Solid Bodies," 1525) had a decisive influence on the cultural region north of the Alps.
0n color perspective, see Rudolf Steiner's lectures of June 2, 1923 (GA 291), and April 19, 1922 (GA 304, p. 208), and the question and answer session of March 11, 1920.

