The Fourth Dimension
GA 324a
31 March 1905, Berlin
Translated by Steiner Online Library
Fifth Lecture
Last time, we tried to get an idea of a four-dimensional space. To visualize it, we reduced it to a three-dimensional one. First, we started by transforming a three-dimensional space into a two-dimensional one. We used colors instead of dimensions. We formed the idea in such a way that a cube appeared in three colors along the three dimensions. Then we laid the boundaries of a cube on the plane, which resulted in six squares in different colors. Through the diversity of colors on the individual sides, we obtained the three different dimensions in two-dimensional space. We had three colors, and with that we had represented the three dimensions.
We then imagined that we were passing a square cube into the third dimension, as if we were passing it through a colored fog and it reappeared on the other side. We imagined that we had pass squares, so that the square cubes move through these squares and are thereby tinged [with the color of the pass square]. This is how we tried to imagine the [three-dimensional] cube [by means of a two-dimensional color representation]. [For the one-dimensional representation of the] surfaces, we thus have two boundary colors and [for the two-dimensional representation of the] cube, three colors. [To represent a four-dimensional spatial structure in three-dimensional space, we must] then add a fourth boundary color.
Now we have to imagine in the same way that a cube, which, analogous to our square, has two different colors as boundary sides, has three different colors in its boundary surfaces. And finally, each cube moves through another cube that has the corresponding fourth color. In doing so, we let it disappear into the fourth color dimension. So, according to Hinton's analogy, we let the respective boundary cubes pass through the new [fourth] color, which then reappears on the other side, emerging in their [original] own color.
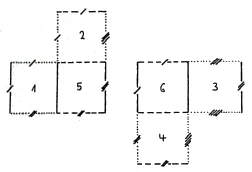
Now I will give you another analogy and first reduce the three dimensions back to two, so that we will then be able to reduce four dimensions to three. To do this, we have to imagine the following. The cube can be put together at its boundary surfaces from its six boundary squares; but instead of doing it in succession, as we did recently, it will now be done in a different way. I will also draw this figure (Figure 31). You see, we have now spread out the cube in two systems, each of which lies in the plane and consists of three squares. Now we have to be clear about how these different areas will lie when we actually put the cube together. I ask you to consider the following. If I now want to reassemble the cube from these six squares, I have to place the two sections on top of each other so that square 6 comes to rest on square 5. When square 5 is placed at the bottom, I have to fold up squares 1 and 2, while folding down squares 3 and 4 (Figure 32). In doing so, we get certain corresponding lines that overlap. The lines marked in the figure with the same color [here in the same line quality and in the same number of lines] will coincide. What lies here in the plane, in two-dimensional space, coincides to a certain extent when I move into three-dimensional space.
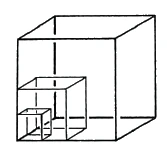
The square consists of four sides, the cube of six squares, and the four-dimensional area would then have to consist of eight cubes.? We call this four-dimensional area a tessaract [after Hinton]. Now, the point is that these eight cubes cannot simply be reassembled into a cube, but that one of them should always pass through the fourth dimension in the appropriate way.
If I now want to do the same with the tessaract as I just did with the cube, I have to follow the same law. The point is to find analogies of the three-dimensional to the two-dimensional and then of the four-dimensional to the three-dimensional. Just as I obtained two systems of [three squares each] here, the same thing happens with the tessaract with [two systems of four cubes each] when I fold a four-dimensional tessaract into three-dimensional space. The system of eight cubes is very ingeniously devised. This structure will then look like this (Figure 33).
Each time, these four cubes in three-dimensional space are to be taken exactly as these squares in two-dimensional space.
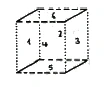
You just have to look carefully at what I have done here. When the cube was folded into two-dimensional space, a system of six squares resulted; when the corresponding procedure is carried out on the tessaract, we obtain a system of eight cubes (Figure 34). We have transferred the observation from three-dimensional space to four-dimensional space. [Folding up and joining the squares in three-dimensional space corresponds to folding up and joining the cubes in four-dimensional space.] In the case of the folded-down cube, [in the two-dimensional plane] different corresponding lines were obtained, which coincided when it was folded up again later. The same occurs with the surfaces of our individual cubes of the tessaract. [When the tessaract is folded down in three-dimensional space, corresponding surfaces appear on the corresponding cubes.] So, for example, in the case of the tessaract, the upper horizontal surface of
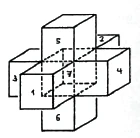
cube 1—by observing [mediation] the fourth dimension—with the front face of cube 5.
In the same way, the right face of cube 1 coincides with the front square of cube 4, and likewise the left square of cube 1 with the front square of cube 3 [as well as the lower square of cube 1 with the front square of cube 6]. The same applies to the other cube surfaces. The remaining cube, 7, is enclosed by the other six.
You see that here again we are concerned with finding analogies between the third and fourth dimensions. Just as a fifth square enclosed by four squares remains invisible to the being that can only see in two dimensions, as we saw in the corresponding figure of the previous lecture (Figure 29), so it is the case here with the seventh cube: it remains hidden from the three-dimensional eye. Corresponding to this seventh cube in the tessaract is an eighth cube, which, since we have a four-dimensional body here, lies as a counterpart to the seventh in the fourth dimension.
All analogies lead us to prepare for the fourth dimension. Nothing forces us to add the other dimensions to the usual dimensions [within the mere spatial view]. Following Hinton, we could also think of colors here and think of cubes put together in such a way that the corresponding colors come together. It is hardly possible in any other way [than by such analogies] to give a description of how to think of a four-dimensional entity.
Now I would like to mention another way [of representing four-dimensional bodies in three-dimensional space], which may also give you a better understanding of what we are actually dealing with here. This is an octahedron bounded by eight triangles, with the sides meeting at obtuse angles (Figure 35).
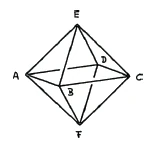
If you visualize this structure here, I ask you to follow the following procedure with me in your mind. You see, here one surface is always intersected by another. Here, for example, in AB, two side surfaces meet, and here in EB, two meet. The entire difference between an octahedron and a cube lies in the angle of intersection of the side surfaces. If surfaces intersect as they do in a cube [at right angles], a cube is formed. But if they intersect as they do here [obtuse], then an octahedron is formed. The point is that we can have surfaces intersect at the most diverse angles, and then we get the most diverse spatial structures."
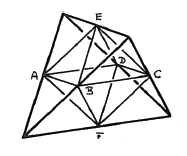
Now imagine that we could also make the same faces of the octahedron intersect in a different way. Imagine this face here, for example AEB, continued on all sides, and this lower one here, BCF, also (Figure 36). Then likewise the ADF and EDC lying backwards. Then these faces must also intersect, and in fact they intersect here in a doubly symmetrical way. If you extend these surfaces in this way, [four of the original boundary surfaces] are no longer needed: ABF, EBC and, towards the back, EAD and DCF. So of the eight surfaces, four remain. And the four that remain give this tetrahedron, which is also called half of an octahedron. It is therefore half of an octahedron because it intersects half of the faces of the octahedron. It is not the case that you cut the octahedron in half. If you bring the other four faces of the octahedron to the cut, the result is also a tetrahedron, which together with the first tetrahedron has the octahedron as a common intersection. In stereometry [geometric crystallography], it is not the part that is halved that is called the half, but the one that is created by halving the [number of] faces. With the octahedron, this is quite easy to imagine.
If you imagine halving the cube in the same way, that is, if you allow one face to intersect with the corresponding other face, you will always get a cube. Half of a cube is a cube again. I would like to draw an important conclusion from this, but first I would like to use something else to help me.
Here I have a rhombic dodecahedron (Figure 37). You can see that the surfaces adjoin each other at certain angles. At the same time, we can see a system of four wires, which I would like to call axial wires, and which run in opposite directions to each other [i.e. connect certain opposite corners of the rhombic dodecahedron, and are therefore diagonals]. These wires now represent a system of axes in a similar way to the way in which you imagined a system of axes on the cube.
You get the cube when you create sections in a system of three perpendicular axes by introducing blockages in each of these axes.
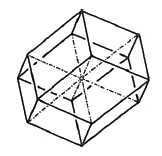
If the axes are made to intersect at other angles, a different spatial figure is obtained. The rhombic dodecahedron has axes which intersect at angles other than right angles.
The cube reflects itself in half.
But this applies only to the cube. The rhombic dodecahedron, cut in half, also gives a different spatial structure.
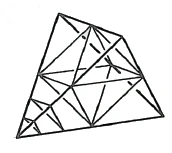
Now let us take the relation of the octahedron to the tetrahedron. And I will tell you what is meant by this. This becomes clear when we gradually let the octahedron merge into the tetrahedron. For this purpose, let us take a tetrahedron, which we cut off at one vertex (Figure 38). We continue this process until the cut surfaces meet at the edges of the tetrahedron; then what remains is the indicated octahedron. In this way we obtain an eight-sided figure from a three-dimensional figure bounded by four surfaces, provided we cut off the corners at corresponding angles.
What I have done here with the tetrahedron, you cannot do with the cube.
The cube has very special properties, namely that it is the counterpart of three-dimensional space. Imagine the entire universe structured in such a way that it has three perpendicular axes. If you then imagine surfaces perpendicular to these three axes, you will, under all circumstances, get a cube (Figure 39). That is why, when we speak of the cube, we mean the theoretical cube, which is the counterpart of three-dimensional space. Just as the tetrahedron is the counterpart of the octahedron when I make the sides of the octahedron into certain sections, so the single cube is the counterpart of the whole of space.” If you think of the whole of space as positive, the cube is negative. The cube is the polar opposite of the whole of space. Space has in the physical cube its actually corresponding structure.
Now suppose I would not limit the [three-dimensional] space by two-dimensional planes, but I would limit it in such a way that I would have it limited by six spheres [thus by three-dimensional figures].
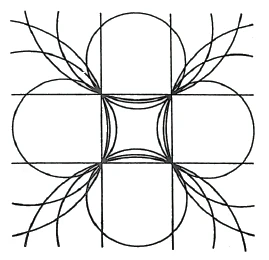
I first define two-dimensional space by having four circles that go inside each other [i.e., two-dimensional shapes]. You can now imagine that these four circles are getting bigger and bigger [as the radius gets longer and longer and the center point moves further and further away]; then, over time, they will all merge into a straight line (Figure 40). You then get four intersecting lines, and instead of the four circles, a square.
Now imagine that the circles are spheres, and that there are six of them, forming a kind of mulberry (Figure 41). If you imagine the spheres in the same way as the circles, that they get larger and larger in diameter, then these six spheres will ultimately become the boundary surfaces of a cube, just as the four circles became the boundary lines of a square.
The cube has now been created from the fact that we had six spheres that have become flat. So the cube is nothing more than a special case of six interlocking spheres – just as the square is nothing more than a special case of four interlocking circles.
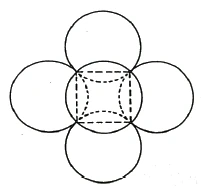
If you are clear in your mind about how to imagine these six spheres, that they correspond to our earlier squares when brought into the plane, and if you imagine an absolutely round shape passing into a straight one, you will get the simplest spatial form. The cube can be imagined as the flattening of six spheres pushed into each other.
You can say of a point on a circle that it must pass through the second dimension if it is to come to another point on the circle. But if you have made the circle so large that it forms a straight line, then every point on the circle can come to every other point on the circle through the first dimension.
We are considering a square bounded by figures, each of which has two dimensions. As long as each of the four boundary figures is a circle, it is therefore two-dimensional. Each boundary figure, when it has become a straight line, is one-dimensional.
Each boundary surface of a cube is formed from a three-dimensional structure in such a way that each of the six boundary spheres has one dimension removed. Such a boundary surface has therefore been created by the third dimension being reduced to two, so to speak bent back. It has therefore lost a dimension. The second dimension was created by losing the dimension of depth. One could therefore imagine that each spatial dimension was created by losing a corresponding higher dimension.
Just as we obtain a three-dimensional figure with two-dimensional boundaries when we reduce three-dimensional boundary figures to two-dimensional ones, so you must conclude that when we look at three-dimensional space, we have to think of each direction as being flattened out, and indeed flattened out from an infinite circle; so that if you could progress in one direction, you would come back from the other. Thus, each [ordinary] spatial dimension has come about through the loss of the corresponding other [dimension]. In our three-dimensional space, there is a three-axis system. These are three perpendicular axes that have lost the corresponding other dimensions and have thus become flat.
So you get three-dimensional space when you straighten each of the [three] axis directions. If you proceed in reverse, each spatial part could become curved again. Then the following series of thoughts would arise: If you curve the one-dimensional structure, you get a two-dimensional one; by curving the two-dimensional structure, you get a three-dimensional one. If you finally curve a three-dimensional structure, you get a four-dimensional structure, so that the four-dimensional can also be imagined as a three-dimensional structure curved on itself.*
And with that, I come from the dead to the living. Through this bending, you can find the transition from the dead to the living. Four-dimensional space is so specialized [at the transition into three dimensions] that it has become flat. Death is [for human consciousness] nothing more than the bending of the three-dimensional into the four-dimensional. [For the physical body taken by itself, it is the other way around: death is a flattening of the four-dimensional into the three-dimensional.]
Fünfter Vortrag
Wir haben das letzte Mal versucht, uns eine Vorstellung eines vierdimensionalen Raumgebildes zu verschaffen. Um es uns zu veranschaulichen, haben wir es auf ein dreidimensionales reduziert. Zunächst sind wir davon ausgegangen, ein dreidimensionales Raumgebilde in ein zweidimensionales zu verwandeln. Wir setzten statt der Dimensionen Farben ein. Wir haben die Vorstellung so ausgebildet, daß ein Würfel längs der drei Dimensionen in drei Farben erschien. Dann legten wir die Grenzen eines Würfels auf die Ebene hin, das ergab uns sechs Quadrate in verschiedenen Farben. Durch die Verschiedenheit der Farben der einzelnen Seiten ergaben sich uns die drei verschiedenen Dimensionen im zweidimensionalen Raum. Wir hatten dreierlei Farben, und damit hatten wir die drei Dimensionen repräsentiert.
Wir haben uns dann vorgestellt, daß wir ein Würfelquadrat in die dritte Dimension hinüberleiten so, wie wenn wir es durch einen farbigen Nebel hinüberleiteten und es auf der anderen Seite wieder erscheint. Wir stellten uns dabei vor, daß wir DurchgangsQuadrate haben, so daß durch diese Quadrate die Würfelquadrate sich hindurchbewegen und sich dadurch [mit der Farbe des Durchgangs-Quadrates] tingieren. So haben wir versucht, uns den [dreidimensionalen] Würfel [vermöge einer zweidimensionalen Farbendarstellung] vorzustellen. [Für die eindimensionale Darstellung der] Flächen haben wir also zwei Grenzfarben und [für die zweidimensionale Darstellung des] Würfels drei Farben. [Um ein vierdimensionales Raumgebilde im dreidimensionalen Raum abzubilden, müssen wir] dann eine vierte Grenzfarbe hinzunehmen.
Nun müssen wir uns in der gleichen Weise vorstellen, daß ein Würfel, der, analog wie unser Quadrat, zwei verschiedene Farben hat als Grenzseiten, drei verschiedene Farben hat in seinen Grenzflächen. Und schließlich bewegt sich jeder Würfel durch einen anderen Würfel, der die entsprechende vierte Farbe hat. Dabei lassen wir ihn also verschwinden in der vierten Farbendimension. Wir lassen also nach der Analogie von Hinton die jeweiligen Grenz-Würfel durch die neue [vierte] Farbe hindurchgehen, die dann auf der anderen Seite wieder erscheinen, auftauchen in ihrer [ursprünglichen] eigenen Farbe.

Nun will ich Ihnen eine andere Analogie geben und zunächst die drei Dimensionen wieder auf zwei reduzieren, so daß wir [anschließend] imstande sein werden, vier Dimensionen auf drei zu reduzieren. Dazu müssen wir uns das folgende vorstellen. Der Würfel kann an seinen Grenzflächen zusammengesetzt werden aus seinen sechs Grenz-Quadraten; statt aber nun, wie neulich, die Ausbreitung hintereinander [zusammenhängend] vorzunehmen, wird sie jetzt auf eine andere Weise geschehen. Ich werde auch diese Figur hinzeichnen (Figur 31). Sie sehen, wir‘haben jetzt auf diese Weise den Würfel ausgebreitet in zwei Systeme, deren jedes in der Ebene liegt und aus je drei Quadraten besteht. Nun müssen wir uns klar werden darüber, wie diese verschiedenen Gebiete liegen werden, wenn wir den Würfel wirklich zusammensetzen. Ich bitte Sie, sich das folgende klar zu machen. Wenn ich nun den Würfel aus diesen sechs Quadraten wieder zusammensetzen will, so muß ich die beiden Abteilungen so übereinanderlegen, daß Quadrat 6 über Quadrat 5 zu liegen kommt. Wenn auf diese Weise Quadrat 5 unten zu liegen kommt, muß ich die Quadrate 1 und 2 hochklappen, die Quadrate 3 und 4 dagegen nach unten hinunterklappen (Figur 32). Dabei bekommen wir also gewisse korrespondierende Linien, die sich gegenseitig decken. Die in der Figur mit gleicher Farbe [hier in gleicher Strichqualität und in gleicher Strichzahl] markierten Linien werden zusammenfallen. Das, was hier in der Ebene, im zweidimensionalen Raum, liegt, fällt in gewisser Weise zusammen, wenn ich in den dreidimensionalen Raum übergehe.

Das Quadrat besteht aus vier Seiten, der Würfel aus sechs Quadraten, und das vierdimensionale Gebiet müßte dann aus acht Würfeln bestehen.? Dieses vierdimensionale Gebiet nennen wir [nach Hinton] Tessarakt. Nun handelt es sich darum, daß diese acht Würfel nicht wiederum einfach zu einem Würfel zusammengesetzt werden dürfen, sondern daß immer einer [dieser acht Würfel] in entsprechender Weise durch die vierte Dimension durchgehen müßte.
Will ich nun dasselbe mit dem Tessarakt machen, was ich eben mit dem Würfel getan habe, so muß ich dasselbe Gesetz einhalten. Es handelt sich darum, Analogien zu finden des Dreidimensionalen zum Zweidimensionalen und dann des Vierdimensionalen zum Dreidimensionalen. Wie ich nun hier zwei Systeme von [je drei] Quadraten erhielt, so ergibt sich beim Tessarakt dasselbe mit [zwei Systemen von je vier] Würfeln, wenn ich ein vierdimensionales Tessarakt in den dreidimensionalen Raum abfalte. Das System von acht Würfeln ist sehr geistreich ausgedacht. Dieses Gebilde wird dann so aussehen (Figur 33).
Dabei sind jedesmal diese vier Würfel im dreidimensionalen Raum genau so zu nehmen, wie diese Quadrate im zweidimensioTa

nalen Raum. Sie müssen sich nur genau anschauen, was ich hier gemacht habe. Bei dem Abklappen des Würfels in den zweidimensionalen Raum ergab sich ein System von sechs Quadraten; bei der entsprechenden Prozedur am Tessarakt erhalten wir ein System von acht Würfeln (Figur 34). Wir haben die Betrachtung für den dreidimensionalen Raum auf den vierdimensionalen Raum übergeführt. [Dem Hochklappen und Zusammenfügen der Quadrate im dreidimensionalen Raum entspricht das Hochklappen und Zusammenfügen der Würfel im vierdimensionalen Raum.] Bei dem abgeklappten Würfel ergaben sich [in der zweidimensionalen Ebene] verschiedene korrespondierende Linien, die sich beim späteren Wiederhochklappen deckten. Ein gleiches findet statt mit den Flächen unserer einzelnen Würfel des Tessaraktes. [Beim abgeklappten Tessarakt im dreidimensionalen Raum ergeben sich bei den entsprechenden Würfeln korrespondierende Flächen.] Es würde also etwa beim Tessarakt die obere horizontale Fläche des

Würfels 1 — durch Beobachtung [Vermittlung] der vierten Dimension — mit der vorderen Fläche des Würfels 5 zusammenfallen.
In gleicher Weise fällt die rechte Fläche des Würfels 1 mit dem vorderen Quadrat des Würfels 4, und ebenso das linke Quadrat des Würfels 1 mit dem vorderen Quadrat des Würfels 3 [sowie das untere Quadrat des Würfels 1 mit dem vorderen Quadrat des Würfels 6] zusammen. [Ganz Entsprechendes gilt für die übrigen Würfelflächen.] Es bleibt übrig der von den sechs anderen eingeschlossene Würfel 7.
Sie sehen, daß es sich hier wieder darum handelt, Analogien zu finden zwischen der dritten und vierten Dimension. Ebenso wie ein von vier Quadraten eingeschlossenes fünftes Quadrat — wie wir dies an der entsprechenden Figur des vorigen Vortrages gesehen haben (Figur 29) - dem nur zweidimensional schauenden Wesen unsichtbar bleibt, so ist dies hier mit dem siebenten Würfel der Fall: er bleibt dem dreidimensionalen Auge verborgen. Diesem siebenten Würfel entspricht beim Tessarakt ein achter Würfel, der, da wir hier einen vierdimensionalen Körper haben, als Gegenstück zum siebenten in der vierten Dimension liegt.
Es laufen alle Analogien darauf hinaus, uns vorzubereiten auf die vierte Dimension. Es zwingt uns nichts, [innerhalb der bloßen Raumesanschauung] zu den gewöhnlichen Dimensionen die anderen Dimensionen [hinzuzufügen]. Im Anschluß an Hinton könnten wir uns auch hier Farben hinzudenken und uns Würfel so zusammengefügt denken, daß die entsprechenden Farben zusammenkommen. Es ist auf eine andere Weise [als durch solche Analogien] kaum möglich, eine Anleitung zu geben, wie man sich ein vierdimensionales Gebilde zu denken hat.
Nun möchte ich noch auf eine andere Weise [der Darstellung vierdimensionaler Körper im dreidimensionalen Raum] zu sprechen kommen, die Ihnen vielleicht auch noch die Möglichkeit geben wird, das besser einzusehen, um was es sich hier eigentlich handelt. Dieses hier ist ein Oktaeder, das von acht Dreiecken begrenzt ist, wobei die Seitenflächen in stumpfen Winkeln aneinanderstoßen (Figur 35).

Wenn Sie sich dieses Gebilde hier vorstellen, so bitte ich Sie, mit mir in Gedanken folgende Prozedur vorzunehmen. Sie sehen, hier ist immer eine Fläche von einer anderen geschnitten. Hier zum Beispiel in AB stoßen zwei Seitenflächen zusammen, und hier in EB stoßen zwei zusammen. Der ganze Unterschied zwischen Oktaeder und Würfel liegt im Schnittwinkel der Seitenflächen. Wenn sich Flächen so wie beim Würfel [rechtwinklig] schneiden, so entsteht ein Würfel. Wenn sie sich aber so schneiden wie hier [stumpf], so entsteht ein Oktaeder. Es handelt sich darum, daß wir Flächen unter den verschiedensten Winkeln sich schneiden lassen, dann bekommen wir die verschiedensten Raumgebilde.”

Denken Sie sich nun, wir könnten hier dieselben Flächen des Oktaeders auch in anderer Weise zum Schneiden bringen. Denken Sie sich diese Fläche hier, zum Beispiel AEB, nach allen Seiten fortgesetzt, und diese untere hier, BCF, auch (Figur 36). Dann ebenso die rückwärts liegenden ADF und EDC. So müssen sich dann diese Flächen ebenfalls schneiden, und zwar schneiden sie sich hier doppelt symmetrisch. Wenn Sie diese Flächen in dieser Weise verlängern, so fallen [vier der ursprünglichen Grenzflächen] fort: ABF, EBC und nach rückwärts EAD und DCF. Von acht Flächen bleiben also vier übrig. Und die vier, die dann bleiben, die geben dieses Tetraeder, das man auch die Hälfte eines Oktaeders nennt. Es ist deshalb die Hälfte eines Oktaeders, weil es die Hälfte der Flächen des Oktaeders zum Schnitt bringt. Es ist also nicht so, daß man das Oktaeder in der Mitte zerschneidet. [Bringt man die übrigen vier Flächen des Oktaeders zum Schnitt, so entsteht ebenfalls ein Tetraeder, das mit dem ersten Tetraeder zusammen genau das Oktaeder als gemeinsames Schnittgebilde besitzt.] In der Stereometrie [geometrischen Kristallographie] bezeichnet man nicht das als die Hälfte, was halbiert wird, sondern das, was durch die Halbierung der [Anzahl der] Flächen entsteht. Beim Oktaeder ist das ganz leicht vorzustellen.
Wenn Sie sich den Würfel in derselben Weise halbiert denken, wenn Sie sich also hier eine Fläche mit der entsprechenden andern sich schneiden lassen, so bekommen Sie immer wieder einen Würfel. Die Hälfte eines Würfels ist wieder ein Würfel. Daraus möchte ich einen wichtigen Schluß ziehen, will aber dazu noch vorher etwas anderes zu Hilfe nehmen.
Hier habe ich einen Rhombenzwölfflächner [Rhombendodekaeder] (Figur 37). Sie sehen, daß die Flächen unter gewissen Winkeln aneinandergrenzen. Es ist nun hier zu gleicher Zeit ein System von vier Drähten zu sehen, welche ich Achsendrähte nennen möchte, und die zueinander gegenläufig sind, [das heißt gewisse einander gegenüberliegende Ecken des Rhombendodekaeders miteinander verbinden, also Diagonalen sind]. Diese Drähte stellen nun in einer ähnlichen Weise ein System von Achsen dar, wie Sie es sich vorstellten, daß am Würfel ein System von Achsen ist.
Den Würfel bekommt man, wenn man bei einem System von drei aufeinander senkrecht stehenden Achsen dadurch Schnittflächen hervorbringt, daß in jeder dieser Achsen Stauungen eintreten.

Läßt man die Achsen unter anderen Winkeln sich schneiden, so bekommt man ein anderes Raumgebilde. Das Rhombendodekaeder hat Achsen, die sich unter anderen als rechten Winkeln schneiden.
Der Würfel gibt halbiert [wieder] sich selbst. Dies trifft aber nur beim Würfel zu. Das Rhombendodekaeder, in seinen halben Flächen zum Schnitt gebracht, gibt ebenfalls ein anderes Raumgebilde.

Nehmen wir nun das Verhältnis des Oktaeders zum Tetraeder. Und zwar will ich Ihnen sagen, was da gemeint ist. Das tritt klar hervor, wenn wir allmählich das Oktaeder in das Tetraeder übergehen lassen. Nehmen wir zu diesem Zwecke ein Tetraeder, dem wir, wie an einer Spitze angedeutet, die Ecken abschneiden (Figur 38). Setzen wir dies fort, bis die Schnittflächen sich an den Kanten des Tetraeders begegnen; dann bleibt übrig das angedeutete Oktaeder. So bekommen wir aus einem Raumgebilde, das durch vier Flächen begrenzt ist, ein achtseitiges Gebilde, wenn wir unter entsprechenden Winkeln die Ecken abschneiden.

Dasselbe, was ich hier mit dem Tetraeder gemacht habe, können Sie wiederum nicht mit dem Würfel machen.*! Der Würfel hat ganz besondere Eigenschaften, nämlich, daß er das Gegenstück ist zum dreidimensionalen Raum. Denken Sie sich den gesamten Weltenraum so gegliedert, daß er drei aufeinander senkrecht stehende Achsen hat. Wenn Sie zu diesen drei Achsen senkrecht stehende Flächen haben, so bekommen Sie unter allen Umständen einen Würfel (Figur 39). Man sagt deshalb, wenn man mit dem Würfel den theoretischen Würfel bezeichnen will, der Würfel sei überhaupt das Gegenstück zum dreidimensionalen Raum. So wie das Tetraeder das Gegenstück ist zum Oktaeder, wenn ich die Seiten des Oktaeders zu bestimmten Schnitten bringe, so ist der einzelne Würfel das Gegenstück zum ganzen Raum.“ Wenn Sie sich den ganzen Raum als positiv denken, so ist der Würfel negativ. Der Würfel ist zum ganzen Raum polar. Der Raum hat im physischen Würfel sein ihm eigentlich korrespondierendes Gebilde.
Nehmen Sie einmal jetzt an, ich würde den [dreidimensionalen] Raum nicht durch zweidimensionale Ebenen begrenzen, sondern ich würde ihn so begrenzen, daß ich ihn durch sechs Kugeln begrenzen lasse [also durch dreidimensionale Gebilde].
Ich begrenze zunächst den zweidimensionalen Raum dadurch, daß ich vier ineinandergehende Kreise [also zweidimensionale Gebilde] habe. Sie können sich nun vorstellen, daß diese vier Kreise immer größer und größer werden [indem der Radius immer länger wird und der Mittelpunkt sich immer weiter entfernt]; dann werden sie mit der Zeit alle in eine gerade Linie übergehen (Figur 40). Sie bekommen dann vier sich schneidende Geraden, und statt der vier Kreise ein Quadrat.

Denken Sie sich nun statt der Kreise Kugeln, und zwar sechs, so daß sie eine Art von Maulbeere bilden (Figur 41). Wenn Sie sich mit den Kugeln dasselbe denken wie mit den Kreisen, daß sie immer größere Durchmesser bekommen, so werden diese sechs Kugeln zuletzt ebenso die Begrenzungsflächen eines Würfels werden, wie die vier Kreise zu Begrenzungslinien eines Quadrates wurden.
Der Würfel ist jetzt dadurch entstanden, daß wir sechs Kugeln hatten, die flach geworden sind. Es ist also der Würfel nichts anderes als der Spezialfall für sechs ineinandergreifende Kugeln — ebenso wie das Quadrat nichts anderes ist als der Spezialfall für vier ineinandergreifende Kreise.

Wenn Sie sich klar sind, daß Sie sich diese sechs Kugeln so vorzustellen haben, daß sie, in die Ebene gebracht, unseren früheren Quadraten entsprechen, wenn Sie sich ein absolut rundes Gebilde übergehend denken in ein gerades, so bekommen Sie die einfachste Raumform. Der Würfel kann vorgestellt werden als die Verflachung von sechs ineinandergeschobenen Kugeln.
Sie können von einem Punkt eines Kreises sagen, daß er durch die zweite Dimension hindurchgehen muß, wenn er zu einem anderen [Punkt des Kreises] kommen will. Haben Sie aber den Kreis so groß werden lassen, daß er eine gerade Linie bildet, dann kann jeder Punkt des Kreises zu jedem anderen Punkt des Kreises kommen durch die erste Dimension.
Wir betrachten ein Quadrat begrenzt von Gebilden, welches jedes zwei Dimensionen hat. Solange jedes von den vier Grenzgebilden ein Kreis ist, ist es also zweidimensional. Jedes Grenzgebilde, wenn es eine Gerade geworden ist, ist eindimensional.
Jede Grenzfläche eines Würfels ist aus einem dreidimensionalen Gebilde so entstanden, daß jeder der sechs Grenzkugeln eine Dimension weggenommen wurde. Eine solche Grenzfläche ist also dadurch entstanden, daß [bei ihr] die dritte Dimension auf zwei reduziert, sozusagen zurückgebogen worden ist. Sie hat also eine Dimension eingebüßt. So ist die zweite Dimension entstanden durch Einbüßung der Tiefen-Dimension. Man könnte also jede Raumesdimension in ihrer Entstehung so vorstellen, daß sie eine entsprechende höhere eingebüßt hat.
Wie wir ein dreidimensionales Gebilde mit zweidimensionalen Grenzen erhalten, wenn wir dreidimensionale Grenzgebilde auf zweidimensionale reduzieren, so müssen Sie daraus schließen, daß wir, wenn wir den dreidimensionalen Raum betrachten, wir eine jede Richtung als verflacht uns zu denken haben, und zwar verflacht aus einem unendlichen Kreis; so daß Sie, wenn Sie in der einen Richtung fortschreiten könnten, Sie aus der anderen zurückkommen würden. So ist eine jede [gewöhnliche] Raumdimension dadurch entstanden, daß sie die entsprechende andere [Dimension] verloren hat. In unserem dreidimensionalen Raum steckt ein dreiachsiges System. Es sind drei aufeinander senkrecht stehende Achsen, welche die entsprechenden anderen Dimensionen eingebüßt haben und dadurch flach geworden sind.
Sie bekommen also den dreidimensionalen Raum, wenn Sie eine jede [der drei] Achsen-Richtungen geradebiegen. Wenn man umgekehrt vorgeht, so könnte jeder Raumteil wieder in sich gekrümmt werden. Dann würde [folgende Gedankenreihe] entstehen: Krümmen Sie das eindimensionale Gebilde, so bekommen Sie ein zweidimensionales; durch Krümmen des zweidimensionalen Gebildes bekommen Sie ein dreidimensionales. Krümmen Sie endlich ein dreidimensionales Gebilde, so bekommen Sie ein vierdimensionales Gebilde, so daß das Vierdimensionale auch vorgestellt werden kann als ein in sich gekrümmtes Dreidimensionales.*
Und damit komme ich von dem Toten zum Lebendigen. Durch dieses Krümmen können Sie den Übergang vom Toten zum Lebendigen finden. Der vierdimensionale Raum ist [beim Übergang ins Dreidimensionale] so spezialisiert, daß er flach geworden ist. Der Tod ist [für das menschliche Bewußtsein] nichts anderes als das Biegen des Dreidimensionalen in das Vierdimensionale. [Für den physischen Leib für sich genommen ist es umgekehrt: Der Tod ist eine Verflachung des Vierdimensionalen in das Dreidimensionale.]

