The Fourth Dimension
GA 324a
7 June 1905, Berlin
Translated by Steiner Online Library
Sixth Lecture
I would like to conclude the lectures on the fourth spatial dimension today if possible, although I would like to demonstrate a complicated system in more detail today. I would have to show you many more models after Hinton; therefore, I can only refer you to the three detailed and spirited books.” Those who do not have the will to form a picture through analogies in the way we have heard it in the past lectures cannot, of course, form a picture of four-dimensional space. It involves a new way of forming thoughts.
I will try to give you a true representation [parallel projection] of the tessaract. You know that in two-dimensional space we had the square, which is bounded by four sides. This is the three-dimensional cube, which is bounded by six squares (Figure 42).
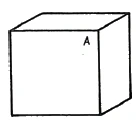
In four-dimensional space, we have the tessaract. A tessaract is bounded by eight cubes. The projection of a tessaract [in three-dimensional space] therefore consists of eight interlocking cubes. We have seen how the [corresponding eight] cubes can be intertwined in three-dimensional space. Today I will show you a [different] way of projecting the tessaract.
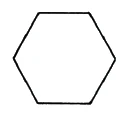
You can imagine that the cube, when held up to the light, throws a shadow on the blackboard. We can mark this shadow figure with chalk (Figure 43). You see that a hexagon is obtained. Now imagine this cube transparent, and you will observe that in the hexagonal figure the three front sides of the cube and the three rear sides of the cube fall into the same plane.
In order to get a projection that we can apply to the tessaract, I would ask you to imagine that the cube is standing in front of you in such a way that the front point A covers the rear point C. If you imagine the third dimension, all this would give you a hexagonal shadow again. I will draw the figure for you (Figure 44).
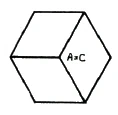
If you imagine the cube like this, you would see the three front surfaces here; the other surfaces would be behind them. The surfaces of the cube appear foreshortened and the angles are no longer right angles. This is how you see the cube depicted so that the surfaces form a regular hexagon. Thus, we have obtained a representation of a three-dimensional cube in two-dimensional space. Since the edges are shortened and the angles are changed by the projection, we must therefore imagine the [projection of the] six boundary squares of the cube as shifted squares, as rhombi.
The same story that I did with a three-dimensional cube that I projected into the plane, we want to do this procedure with a four-dimensional spatial object, which we therefore have to place in three-dimensional space. We must therefore bring the structure composed of eight cubes, the tessaract, into the third dimension [by parallel projection]. With the cube, we obtained three visible and three invisible edges, all of which enter into the space and in reality do not lie within the [projection] surface. Now imagine a cube shifted in such a way that it becomes a rhombicuboctahedron.” Take eight of these figures, and you have the possibility of combining the eight [boundary] cubes of the tessaract in such a way that, when pushed together, they form the eight (doubly covered) rhombicuboctahedra of this spatial figure (Figure 45).
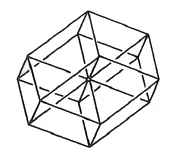
Now you have one more axis here [than in the three-dimensional cube]. Accordingly, a four-dimensional spatial structure naturally has four axes. So if we push it together, four axes still remain. There are eight [pushed together] cubes in this projection, which are represented as rhombicuboctahedra. The rhombicuboctahedron is a [symmetrical] image or silhouette of the tessaract in three-dimensional space.
We arrived at this relationship by means of an analogy, but it is completely correct: just as we obtained a projection of the cube onto a plane, it is also possible to represent the tessaract in three-dimensional space by means of a projection. It behaves in the same way as the silhouette of the cube in relation to the cube itself. I think that is quite easy to understand.
Now I would like to tie in with the greatest image that has ever been given for this, namely Plato and Schopenhauer and the parable of the cave.
Plato says: Imagine people sitting in a cave, and they are all tied up so that they cannot turn their heads and can only look at the opposite wall. Behind them are people carrying various objects past them. These people and these objects are three-dimensional. So all these [bound] people stare at the wall and see only what is cast as a shadow [of the objects] on the wall. So they would see everything in the room only as a shadow on the opposite wall as two-dimensional images.
Plato says that this is how it is in the world in general. In truth, people are sitting in the cave. Now, people themselves and everything else are four-dimensional; but what people see of it are only images in three-dimensional space.
This is how all the things we see present themselves. According to Plato, we are dependent on seeing not the real things, but the three-dimensional silhouettes. I only see my hand as a silhouette; in reality it is four-dimensional, and everything that people see of it is just as much an image of it as what I just showed you as an image of the Tessaract. Thus Plato was already trying to make clear that the objects we know are actually four-dimensional, and that we only see silhouettes of them in three-dimensional space. And that is not entirely arbitrary. I will give you the reasons for this in a moment.
Of course, anyone can say from the outset that this is mere speculation. How can we even imagine that the things that appear on the wall have a reality? Imagine that you are sitting here in a row, and you are sitting very still. Now imagine that the things on the wall suddenly start to move. You will not be able to tell yourself that the images on the wall can move without going out of the second dimension. If something moves there, it indicates that something must have happened outside the wall, on the real object, for it to move at all. That's what you tell yourself. If you imagine that the objects in three-dimensional space can pass each other, this would not be possible with their two-dimensional silhouettes, if you think of them as substantial, that is, impenetrable. If those images, conceived substantially, wanted to move past each other, they would have to go out of the second dimension.
As long as everything on the wall is at rest, I have no reason to conclude that something is happening outside the wall, outside the space of the two-dimensional silhouettes. But the moment history begins to move, I must investigate the source of the motion. And you realize that the change can only come from motion outside the wall, only from motion within a third dimension. The change has thus told us that there is a third dimension in addition to the second.
What is a mere image also has a certain reality, possesses very definite properties, but differs essentially from the real object. You will not be able to deny that the mirror image is also a mere image. You see yourself in the mirror, and you are also there. If there is not a third [that is, an active being] there, then you could not actually know what you are. But the mirror image makes the same movements that the original makes; the image is dependent on the real object, the being; it itself has no ability [to move]. Thus, a distinction can be made between image and being in that only a being can bring about movement and change out of itself. I realize from the shadows on the wall that they cannot move themselves, so they cannot be beings. I have to go out of them if I want to get to the beings.
Now apply this to the world in general. The world is three-dimensional. Take this three-dimensional world for itself, as it is; grasp it completely in your thoughts [for yourself], and you will find that it remains rigid. It remains three-dimensional even if you suddenly think the world frozen at a certain point in time. But there is no one and the same world in two points in time. The world is completely different at successive points in time. Imagine that these points in time cease to exist, so that what is there remains. Without time, no change would occur in the world. The world would remain three-dimensional even if it underwent no change at all. The pictures on the wall also remain two-dimensional. But change suggests a third dimension. The fact that the world is constantly changing, and that it remains three-dimensional even without change, suggests that we have to look for the change in a fourth dimension. We have to look for the reason, the cause of the change, the activity outside the third dimension, and with that you have initially uncovered the fourth of the dimensions. But with that you also have the justification for Plato's image. So we understand the whole three-dimensional world as the shadow projection of a four-dimensional world. The only question is how we have to take this fourth dimension [in reality].
You see, we have the one idea to make it clear to ourselves, of course, that it is impossible for the fourth dimension to fall [directly] into the third. That is not possible. The fourth dimension cannot fall into the third. I would like to show you now how one can, so to speak, get an idea of how to go beyond the third dimension. Imagine we have a circle – I have already tried to evoke a similar idea recently – if you imagine this circle getting bigger and bigger, then a piece of this circle becomes flatter and flatter, and because the diameter of the circle becomes very large at the end, the circle finally turns into a straight line. The line has one dimension, but the circle has two dimensions. How do you get a second dimension from a single dimension? By curving a straight line, you get a circle again.
If you now imagine the surface of the circle curving into space, you first get a shell, and if you continue to do this, you get a sphere. Thus a line acquires a second dimension by curvature and a surface acquires a third dimension by curvature. If you could now curve a cube, it would have to be curved into the fourth dimension, and you would have the [spherical] tessaract.
You can understand the sphere as a curved two-dimensional spatial structure. The sphere that occurs in nature is the cell, the smallest living thing. The cell is limited spherically. That is the difference between the living and the lifeless. The mineral always occurs as a crystal bounded by flat surfaces; life is bounded by spherical surfaces, built up of cells. That means that just as a crystal is built from spheres that have been straightened out, that is, from planes, so life is built from cells, that is, from spheres that have been bent together. The difference between the living and the dead lies in the way they are defined. The octahedron is defined by eight triangles. If we imagine the eight sides as spheres, we would get an eight-limbed living thing.
If you curve the three-dimensional structure, the cube, again, you get a four-dimensional structure, the spherical tessaract. But if you curve the whole space, you get something that relates to three-dimensional space in the same way that a sphere relates to a plane.
Just as the cube, as a three-dimensional structure, is bounded by planes, so every crystal is bounded by planes. The essence of a crystal is the assembly of [flat] boundary planes. The essence of the living is the assembly of curved surfaces, of cells. The assembly of something even higher would be a structure whose individual boundaries would be four-dimensional. A three-dimensional structure is bounded by two-dimensional structures. A four-dimensional being, that is, a living being, is bounded by three-dimensional beings, by spheres and cells. A five-dimensional being is itself bounded by four-dimensional beings, by spherical tessaracts. From this you can see that we have to ascend from three-dimensional to four-dimensional, and then to five-dimensional beings.
We only have to ask ourselves: What must occur in a being that is four-dimensional?* A change must occur within the third dimension. In other words: If you hang pictures on the wall here, they are two-dimensional and generally remain static. But if you have pictures in which the second dimension moves and changes, then you must conclude that the cause of this movement can only lie outside the surface of the wall, that the third dimension of space thus indicates the change. If you find changes within the third spatial dimension itself, then you must conclude that a fourth dimension is involved, and this brings us to the beings that undergo a change within their three spatial dimensions.
It is not true that we have fully recognized a plant if we have only recognized it in its three dimensions. A plant is constantly changing, and this change is an essential, a higher characteristic of it. The cube remains; it only changes its shape when you smash it. A plant changes its shape itself, that is, there is something that is the cause of this change and that lies outside the third dimension and is an expression of the fourth dimension. What is that?
You see, if you have this cube and draw it, you would labor in vain if you wanted to draw it differently at different moments; it will always remain the same. If you draw the plant and compare the picture with your model after three weeks, it will have changed. So this analogy is completely accurate. Everything that lives points to something higher, where it has its true essence, and the expression of this higher is time. Time is the symptomatic expression, the appearance of liveliness [understood as the fourth dimension] in the three dimensions of physical space. In other words, all beings for whom time has an inner meaning are images of four-dimensional beings. This cube is still the same after three or six years. The lily bud changes. Because for it, time has a real meaning. Therefore, what we see in the lily is only the three-dimensional image of the four-dimensional lily being. So time is an image, a projection of the fourth dimension, the organic liveliness, into the three spatial dimensions of the physical world.
To understand how a following dimension relates to the preceding one, please imagine the following: a cube has three dimensions; when you visualize the third, you have to remember that it is perpendicular to the second, and the second is perpendicular to the first. The three dimensions are characterized by the fact that they are perpendicular to one another. But we can also imagine how the third dimension arises from the following [fourth dimension]. Imagine that you would change the cube by coloring the boundary surfaces and then changing these colors [in a certain way, as in Hinton's example]. Such a change can indeed be made, and it corresponds exactly to the change that a three-dimensional being undergoes when it passes into the fourth dimension, when it develops through time. If you cut a four-dimensional being at any point, you take away the fourth dimension, you destroy it. If you do that to a plant, you do exactly the same thing as if you were to make a cast of the plant, a plaster cast. You have captured that by destroying the fourth dimension, time. Then you get a three-dimensional object. If for any three-dimensional being the fourth dimension, time, has an essential significance, then it is a living being.
Now we enter the fifth dimension. You can say to yourself that you must again have a boundary that is perpendicular to the fourth dimension. We have seen that the fourth dimension is related to the third dimension in a similar way to the third dimension being related to the second. It is not immediately possible to visualize the fifth dimension in this way. But you can again create a rough idea by using an analogy. How does a dimension come into being in the first place? If you simply draw a line, you will never create another dimension by simply pushing the line in one direction. Only by imagining that you have two opposing directions of force, which then accumulate at a point, only by expressing the accumulation, do you have a new dimension. We must therefore be able to grasp the new dimension as a new line of accumulation [of two currents of force], and imagine the one dimension coming from the right one time and from the left the next, as positive and negative. So I understand a dimension [as a polar [stream of forces] within itself], so that it has a positive and a negative dimension [component], and the neutralization [of these polar force components] is the new dimension.
From there, we want to create an idea of the fifth dimension. We will have to imagine that the fourth dimension, which we have found expressed as time, behaves in a positive and negative way. Now take two beings for whom time has a meaning, and imagine two such beings colliding with each other. Then something must appear as a result, similar to what we have previously called an accumulation of [opposing] forces; and what arises as a result when two four-dimensional beings come into relation with each other is their fifth dimension. This fifth dimension arises as a result, as a consequence of an exchange [a neutralization of polar force effects], in that two living beings, through their mutual interaction, produce something that they do not have outside [in the three ordinary spatial dimensions together], nor do they have in [the fourth dimension,] time, but have completely outside these [previously discussed dimensions or] boundaries. This is what we call compassion [or feeling], by which one being knows another, thus the realization of the [spiritual and mental] inner being of another being. A being could never know anything about another being outside of time [and space] if you did not add a higher, fifth dimension, [i.e. enter the world of] sensation. Of course, here the sensation is only to be understood as a projection, as an expression [of the fifth dimension] in the physical world.
Developing the sixth dimension in the same way would be too difficult, so I will only indicate it. [If we tried to progress in this way, something could be developed as an expression of the sixth dimension that,] when placed in the three-dimensional physical world, is self-conscious.
Man, as a three-dimensional being, is one who shares his imagery with other three-dimensional beings. The plant, in addition, has the fourth dimension. For this reason, you will never find the ultimate essence of the plant within the three dimensions of space, but you would have to ascend from the plant to a fourth spatial dimension [to the astral sphere]. But if you wanted to grasp a being that has feeling, you would have to ascend to the fifth dimension [to the lower Devachan, to the Rupa sphere]; and if you wanted to grasp a being that has self-awareness, a human being, you would have to ascend to the sixth dimension [to the upper Devachan, to the Arupa sphere]. Thus, the human being as he stands before us in the present is indeed a six-dimensional being. That which is called feeling or compassion, or self-awareness, is a projection of the fifth or sixth dimension into ordinary three-dimensional space. Man extends into these spiritual spheres, albeit unconsciously for the most part; only there can he actually be experienced in the sense indicated last. This six-dimensional being can only come to an idea of even the higher worlds if it tries to get rid of the actual characteristics of the lower dimensions.
I can only hint at the reason why man considers the world to be only three-dimensional, namely because he is conditioned in his perception to see only a reflection of something higher in the world. When you look in a mirror, you also see only a reflection of yourself. Thus, the three dimensions of our physical space are indeed reflections, material copies of three higher, causally creative dimensions. Our material world therefore has its polar [spiritual] counter-image in the group of the three next higher dimensions, that is, in those of the fourth, fifth and sixth dimensions. And in a similar sense, the spiritual worlds that lie beyond this group of dimensions, which can only be sensed, are also polar to those of the fourth to sixth dimensions.
If you have water and you let the water freeze, the same substance is present in both cases; but in form they differ quite substantially. You can imagine a similar process for the three higher dimensions of man. If you think of man as a purely spiritual being, then you have to think of him as having only the three higher dimensions – self-awareness, feeling and time – and these three dimensions are reflected in the physical world in its three ordinary dimensions.
The yogi [secret student], if he wants to advance to a knowledge of the higher worlds, must gradually replace the mirror images with reality. For example, when he looks at a plant, he must get used to gradually substituting the higher dimensions for the lower ones. If he looks at a plant and is able to abstract from one spatial dimension in the case of a plant, to abstract from one spatial dimension and instead to imagine a corresponding one of the higher dimensions, in this case time, then he actually gets an idea of what a two-dimensional, moving being is. To make this being more than just an image, to make it correspond to reality, the yogi must do the following. If he disregards the third dimension and adds the fourth, he would only get something imaginary. However, the following mental image can help: when we make a cinematographic representation of a living being, we remove the third dimension from the original three-dimensional processes, but add the [dimension of] time through the sequence of images. If we then add sensation to this [moving] perception, we perform a procedure similar to what I described earlier as the bending of a three-dimensional structure into the fourth dimension. Through this process you then get a four-dimensional entity, but now one that has two of our spatial dimensions, but also two higher ones, namely time and sensation. Such beings do indeed exist, and these beings - and this brings me to a real conclusion to the whole consideration - I would like to tell you about.
Imagine two spatial dimensions, that is, a surface, and this surface endowed with motion. Now imagine a bent as a sensation, a sentient being that then pushes a two-dimensional surface in front of it. Such a being must act differently and be very different from a three-dimensional being in our space. This flat creature that we have constructed in this way is incomplete in one direction, completely open, and offers you a two-dimensional view; you cannot go around it, it comes towards you. This is a luminous creature, and the luminous creature is nothing other than the incompleteness in one direction.
Through such a being, the initiates then get to know other beings, which they describe as divine messengers approaching them in flames of fire. The description of Mount Sinai, where Moses received the Ten Commandments,® means nothing other than that a being could indeed approach him that, to his perception, had these dimensions. It appeared to him like a human being from whom the third spatial dimension had been removed; it appeared in sensation and in time.
These abstract images in the religious documents are not just external symbols, but powerful realities that man can get to know if he is able to appropriate what we have tried to make clear through analogies. The more you devote yourself diligently and energetically to such considerations of analogies, the more you really work on your mind, and the more these [considerations] work in us and trigger higher abilities. [This is roughly the case when dealing with] the analogy of the relationship of the cube to the hexagon and the tessaract to the rhombic dodecahedron. The latter represents a projection of the tessaract into the three-dimensional physical world. If you visualize these figures as living entities, if you allow the cube to grow out of the projection of the die – the hexagon – and likewise allow the tessaract itself to arise from the projection of the tessaract [the rhombic dodecahedron], then you create the possibility and the ability in your lower mental body to grasp what I have just described to you as a structure. And if, in other words, you have not only followed me but have gone through this procedure vividly, as the yogi does in an awakened state of consciousness, then you will notice that something will occur to you in your dreams that in reality is a four-dimensional entity, and then it is not much further to bring it over into the waking consciousness, and you can then see the fourth dimension in every four-dimensional being.
The astral sphere is the fourth dimension. Devachan to rupa is the fifth dimension. Devachan to arupa is the sixth dimension.
These three worlds, the physical, astral and celestial [devachan], comprise six dimensions. The even higher worlds are completely polar to these.
Mineral Plant Animal Human Arupa Self-consciousness Rupa Sensation Self-consciousness Astral plane Life Sensation Self-consciousness Physical form Life Sensation Self-plan consciousness Form Life Sensation Form Life Form
Sechster Vortrag
Ich möchte heute möglichst die Vorträge über die vierte Raumdimension zum Abschluß bringen, obwohl ich heute noch eingehender ein kompliziertes System vorführen möchte. Ich müßte nach Hinton Ihnen noch viele Modelle anführen; ich kann Sie deshalb nur auf die drei ausführlichen und geistvollen Bücher verweisen.“ Wer nicht den Willen hat, sich durch Analogien in der Weise ein Bild zu machen, wie wir es in den vergangenen Vorträgen gehört haben, kann sich natürlich keine Vorstellung vom vierdimensionalen Raum machen. Es handelt sich um eine neue Art der Gedankenbildung.
Ich will Ihnen eine wirkliche Abbildung [Parallelprojektion] des Tessaraktes verschaffen. Sie wissen, wir hatten im zweidimensionalen Raum das Quadrat, das von vier Seiten begrenzt ist. Dies ist der dreidimensionale Würfel, der durch sechs Quadrate begrenzt ist (Figur 42).

Im vierdimensionalen Raum haben wir das Tessarakt. Ein Tessarakt ist von acht Würfeln begrenzt. Die Projektion eines Tessaraktes [in den dreidimensionalen Raum] besteht folglich aus acht ineinandergeschobenen Würfeln. Wir haben gesehen, wie im dreidimensionalen Raum die [entsprechenden acht] Würfel miteinander verschlungen werden können. Heute will ich Ihnen eine [andere] Art Projektion des Tessaraktes machen.
Sie können sich vorstellen, daß der Würfel, wenn er gegen das Licht gehalten wird, einen Schatten auf die Tafel wirft. Diese seine Schattenfigur können wir mit Kreide festhalten (Figur 43). Sie sehen, es kommt dabei ein Sechseck heraus. Nun denken Sie sich einmal diesen Würfel durchsichtig, so würden Sie zu beachten haben, daß in der sechseckigen Figur die drei vorderen Würfelseiten und die drei hinteren Würfelseiten in dieselbe Fläche hineinfallen.

Damit wir nun eine Projektion bekommen können, die wir auf das Tessarakt anwenden können, bitte ich Sie sich zu denken, daß der Würfel so vor Ihnen steht, daß der vordere Punkt A den hinteren Punkt C zudeckt. Das alles würde Ihnen, wenn Sie sich die dritte Dimension fortdenken, wieder einen sechseckigen Schatten geben. Ich will Ihnen dafür die Figur hinzeichnen (Figur 44).

Den Würfel so gedacht, würden Sie hier die drei vorderen Flächen sehen; die anderen Flächen würden dahinter liegen. Die Flächen des Würfels erscheinen Ihnen dabei verkürzt und die Winkel nicht mehr als rechte. So sehen Sie den Würfel so abgebildet, daß er für den Flächenanblick ein reguläres Sechseck ergibt. So haben wir im zweidimensionalen Raum eine Abbildung eines dreidimensionalen Würfels bekommen. Da durch die Projektion die Kanten verkürzt und die Winkel verändert werden, müssen wir uns also die [Projektion der] sechs Grenz-Quadrate des Würfels als verschobene Quadrate, als Rhomben vorstellen.
Dieselbe Geschichte, die ich mit einem dreidimensionalen Würfel machte, den ich in die Ebene hineinprojizierte, diese Prozedur wollen wir mit einem vierdimensionalen Raumgebilde machen, das wir also in den dreidimensionalen Raum hineinlegen müssen. Wir müssen also das aus acht Würfeln zusammengesetzte Gebilde, das Tessarakt, [durch Parallelprojektion] in die dritte Dimension hineinbringen. Wir haben bei dem Würfel drei sichtbare und drei unsichtbare Kanten bekommen, die alle in den Raum hineingehen und in Wirklichkeit nicht in der [Projektions]fläche drinnenliegen. Denken Sie sich nun einen Würfel so verschoben, daß daraus ein Rhombenwürfel wird.” Nehmen Sie acht dieser Gebilde, so haben Sie die Möglichkeit, die acht [Grenz-]Würfel des Tessaraktes so zusammenzulegen, daß sie zusammengeschoben [die] acht [doppelt überdeckten] Rhomben-Würfel dieses Raumgebildes [des Rhombendodekaeders] ergeben (Figur 45).

Nun haben Sie hier eine Achse mehr [als beim dreidimensionalen Würfel]. Ein vierdimensionales Raumgebilde hat dementsprechend natürlich vier Achsen. Wenn wir es uns also zusammenschieben, so bleiben immer noch vier Achsen übrig. Es stecken dabei in dieser Projektion acht [zusammengeschobene] Würfel, die sich darin als Rhombenwürfel darstellen. Das Rhombendodekaeder ist ein [symmetrisches] Abbild oder Schattenbild des Tessaraktes im dreidimensionalen Raum.
Wir sind [zu diesen Beziehungen] durch eine Analogie gekommen, die aber vollständig stimmt: ebenso wie wir eine Projektion des Würfels in die Fläche bekommen haben, ebenso kann man tatsächlich das Tessarakt im dreidimensionalen Raum durch eine Projektion darstellen. Sie verhält sich ebenso wie das Schattenbild des Würfels zum Würfel selbst. Ich glaube, das ist ganz gut zu verstehen.
Nun möchte ich gleich an das großartigste Bild anknüpfen, das je dafür gegeben worden ist, nämlich an Plato und Schopenhauer und das Gleichnis mit der Höhle.
Plato sagt: Man denke sich einmal in einer Höhle Menschen sitzen, und zwar sind sie alle so gefesselt, daß sie den Kopf nicht drehen und nur nach der gegenüberliegenden Wand schauen können. Hinter ihnen befinden sich Menschen, die die verschiedensten Gegenstände vorübertragen. Diese Menschen und diese Gegenstände sind dreidimensional. Alle diese [gefesselten] Menschen starren also auf die Wand und sehen nur das, was als Schattenbild [von den Gegenständen] auf die Wand geworfen wird. So würden Sie alles, was hier im Zimmer ist, nur als Schatten an der gegenüberliegenden Wand als zweidimensionale Bilder wieder sehen.
Nun sagt Plato: So ist es überhaupt in der Welt. In Wahrheit sitzen die Menschen in der Höhle. Nun sind die Menschen selbst und alles übrige vierdimensional; aber was die Menschen davon sehen, sind nur Bilder im dreidimensionalen Raum.
So stellen sich alle Dinge dar, die wir überhaupt sehen. Gemäß Plato sind wir darauf angewiesen, nicht die wirklichen Dinge, sondern die dreidimensionalen Schattenbilder zu sehen. Meine Hand sehe ich nur als Schattenbild, sie ist in Wahrheit vierdimensional, und alles, was die Menschen davon sehen, ist ebenso das Abbild davon, wie das, was ich Ihnen eben als Abbild des Tessaraktes gezeigt habe. So suchte Plato schon damals klarzumachen, daß die Körper, die wir kennen, eigentlich vierdimensional sind, und daß wir von ihnen nur Schattenbilder im dreidimensionalen Raum sehen. Und das ist nicht ganz willkürlich. Dafür will ich Ihnen gleich die Gründe anführen.
Von vornherein kann natürlich jeder sagen, das sei eine bloße Spekulation. Wie können wir uns überhaupt eine Vorstellung davon machen, daß diese Dinge, die dort an der Wand erscheinen, eine Realität haben? Denken Sie sich einmal, Sie sitzen hier in einer Reihe, und Sie sitzen ganz starr. Denken Sie sich jetzt aber, daß die Dinge sich plötzlich anfangen zu bewegen. Sie werden unmöglich sich sagen können, daß die Bilder auf der Wand sich bewegen können, ohne daß aus der zweiten Dimension herausgegangen wird. Wenn sich dort etwas bewegt, so deutet das darauf hin, daß außerhalb der Wand, an dem wirklichen Objekt, etwas geschehen sein muß, damit es sich überhaupt bewegt. Das sagen Sie sich. [Wenn man sich vorstellt, daß] die Objekte im dreidimensionalen Raum nebeneinander vorbeigehen können, wäre dies mit ihren zweidimensionalen Schattenbildern nicht möglich, falls man sich dieselben substantiell, das heißt undurchdringlich denkt. Wenn sich jene Bilder, substantiell gedacht, nebeneinander vorbei bewegen wollten, so müßten sie aus der zweiten Dimension hinausgehen.
Solange alles in Ruhe ist auf der Wand, habe ich keine Veranlassung, auf irgendein Geschehen außerhalb der Wand, außerhalb des Raumes der zweidimensionalen Schattenbilder, zu schließen. Im Augenblick aber, wo die Geschichte anfängt sich zu bewegen, muß ich untersuchen, woher die Bewegung kommt. Und Sie sagen sich, daß die Veränderung nur von einer Bewegung außerhalb der Wand herstammen kann, nur kommen kann aus der Bewegung innerhalb einer dritten Dimension. Die Veränderung hat uns also gesagt, daß es außer einer zweiten noch eine dritte Dimension gibt.
Was bloßes Bild ist, hat auch eine gewisse Realität, besitzt ganz bestimmte Eigenschaften, unterscheidet sich aber wesentlich von dem wirklichen Gegenstande. Sie werden nicht ableugnen können, daß auch das Spiegelbild ein bloßes Bild ist. Sie sehen im Spiegel sich, und Sie sind außerdem auch noch da. Ist nun [nicht noch] ein drittes [das heißt ein wirksames Wesen] da, so könnten Sie tatsächlich nicht wissen, was Sie sind. Aber das Spiegelbild macht dieselben Bewegungen, die das Original macht; das Bild ist abhängig von dem wirklichen Gegenstande, dem Wesen; es hat selbst keine Fähigkeit [sich zu bewegen]. Es kann also unterschieden werden zwischen Bild und Wesen dadurch, daß nur ein Wesen aus sich selbst heraus Bewegung, Veränderung zustande bringen kann. Von den Schattenbildern auf der Wand werde ich gewahr, daß sie sich selbst nicht bewegen können, sie also keine Wesen sein können. Ich muß aus ihnen herausgehen, wenn ich zu den Wesen kommen will.
Wenden Sie das nun auf die Welt überhaupt an. Die Welt ist dreidimensional. Nehmen Sie diese dreidimensionale Welt einmal für sich, so wie sie ist; fassen Sie sie in Gedanken ganz [für sich selbst], und Sie werden finden, daß sie starr bleibt. Sie bleibt noch dreidimensional, auch wenn Sie die Welt in einem bestimmten Zeitpunkte sich plötzlich eingefroren denken. Es gibt aber nicht in zwei Zeitpunkten ein und dieselbe Welt. Die Welt ist in den aufeinanderfolgenden Zeitpunkten durchaus verschieden. Denken Sie sich, daß diese Zeitpunkte fortfielen, so daß das bleibt, was da ist. Ohne die Zeit geschähe gar keine Veränderung mit der Welt. Die Welt bliebe eine dreidimensionale auch dann, wenn sie gar keine Veränderung durchmachte. Die Bilder auf der Wand bleiben auch zweidimensional. Aber die Veränderung deutet auf eine dritte Dimension hin. Daß sich die Welt fortwährend ändert, und daß sie auch ohne Veränderung dreidimensional bleibt, deutet darauf hin, daß wir die Veränderung in einer vierten Dimension suchen müssen. Den Grund, die Ursache der Veränderung, die Tätigkeit müssen wir außerhalb der dritten Dimension suchen, und damit haben Sie die vierte der Dimensionen zunächst einmal erschlossen. Damit haben Sie aber auch die Rechtfertigung für das Bild Platos. So fassen wir die ganze dreidimensionale Welt auf als die Schattenprojektion einer vierdimensionalen Welt. Es fragt sich nur, wie wir diese vierte Dimension [in Wirklichkeit] zu nehmen haben.
Sehen Sie, wir haben die eine Vorstellung uns natürlich klar zu machen, daß es unmöglich ist, daß die vierte Dimension [unmittelbar] in die dritte hineinfällt. Das geht nicht. Die vierte Dimension kann nicht in die dritte hineinfallen. Ich möchte Ihnen einmal jetzt zeigen, wie man sozusagen darüber einen Begriff bekommen kann, wie man über die dritte Dimension hinauskommt. Wenn Sie sich einmal vorstellen, daß wir einen Kreis haben — ich habe schon letzthin eine ähnliche Vorstellung wachzurufen versucht” - wenn Sie sich diesen Kreis immer größer und größer werdend denken, so wird ein Stück dieses Kreises immer flacher und flacher, und dadurch, daß der Durchmesser des Kreises zuletzt ganz groß wird, geht der Kreis endlich über in eine gerade Linie. Die Linie hat eine Dimension, der Kreis aber hat zwei Dimensionen. Wie bekommen Sie nun wieder aus einer Dimension eine zweite? Durch Krümmung einer geraden Linie erhalten Sie wieder einen Kreis.
Wenn Sie sich nun die Kreisfläche in den Raum hineingekrümmt denken, so bekommen Sie erst mal eine Schale, und wenn Sie dies noch weiter machen, eine Kugel. So bekommt eine Linie durch Krümmung eine zweite Dimension und eine Fläche durch Krümmung eine dritte Dimension. Wenn Sie nun einen Würfel noch krümmen könnten, so müßte er in die vierte Dimension hineingekrümmt werden, und Sie hätten das [sphärische] Tessarakt.
Die Kugel können Sie auffassen als ein gekrümmtes zweidimensionales Raumgebilde. Die Kugel, die in der Natur auftritt, ist die Zelle, das kleinste Lebewesen. Die Zelle begrenzt sich kugelig. Das ist der Unterschied zwischen dem Lebendigen und dem Leblosen. Das Mineral tritt als Kristall immer von ebenen Flächen begrenzt auf; das Leben ist begrenzt von kugeligen Flächen, aufgebaut aus Zellen. Das heißt, so wie ein Kristall aufgebaut ist aus geradegebogenen Kugeln, das heißt Ebenen, so ist das Leben aufgebaut aus Zellen, also aus zusammengekrümmten Kugeln. Der Unterschied zwischen Lebendigem und Totem liegt in der Art und Weise der Begrenzung. Das Oktaeder ist begrenzt von acht Dreiecken. Wenn wir uns die acht Seiten aus Kugeln zusammengesetzt denken, so würden wir ein achtgliedriges Lebendiges erhalten.
Wenn Sie gleichsam das dreidimensionale Gebilde, den Würfel, nochmals krümmen, so bekommen Sie ein vierdimensionales Gebilde, das sphärische Tessarakt. Krümmen Sie aber den ganzen Raum, so erhalten Sie etwas, was sich zum dreidimensionalen Raum so verhält, wie sich die Kugel zur Ebene verhält.
Wie nun der Würfel als dreidimensionales Gebilde von Ebenen begrenzt ist, so ist überhaupt jeder Kristall von Ebenen begrenzt. Das Wesentliche eines Kristalles ist die Zusammenfügung aus [flachen] Grenz-Ebenen. Das Wesentliche des Lebendigen ist die Zusammenfügung aus gekrümmten Flächen, aus Zellen. Die Zusammenfügung eines noch Höheren würde ein solches Gebilde sein, dessen einzelne Grenzen vierdimensional sein würden. Ein dreidimensionales Gebilde ist begrenzt von zweidimensionalen Gebilden. Ein vierdimensionales Wesen, das heißt ein lebendiges Wesen, ist begrenzt von dreidimensionalen Wesen, von Kugeln und Zellen. Ein fünfdimensionales Wesen ist selbst begrenzt von vierdimensionalen Wesen, von sphärischen Tessarakten. Daraus sehen Sie, daß wir aufsteigen müssen von dreidimensionalen zu vierdimensionalen, und dann zu fünfdimensionalen Wesen.
Wir müssen uns nur fragen: Was muß eintreten bei einem Wesen, das vierdimensional ist?* Es muß dabei innerhalb der dritten Dimension eine Veränderung eintreten. Mit anderen Worten: Hängen Sie hier an die Wand Bilder, so sind diese zweidimensional, sie bleiben im allgemeinen starr. Haben Sie aber Bilder, die sich in der zweiten Dimension bewegen, verändern, so müssen Sie schließen, daß die Ursache dieser Bewegung nur außerhalb der Wandfläche liegen kann, daß also die dritte Raumdimension die Veränderung angibt. Finden Sie Veränderungen innerhalb der dritten Raumesdimension selbst, so müssen Sie schließen, daß eine vierte Dimension zugrunde liegt, und damit kommen wir zu den Wesen, die eine Veränderung innerhalb ihrer drei Raumdimensionen durchmachen.
Es ist nicht wahr, daß wir eine Pflanze ganz erkannt haben, wenn wir sie nur in ihren drei Dimensionen erkannt haben. Eine Pflanze verändert sich fortwährend, und diese Veränderung ist ein wesentliches, ein höheres Merkmal derselben. Der Würfel bleibt; er ändert seine Form nur, wenn Sie ihn zerschlagen. Ein Pflanze ändert ihre Form selbst, das heißt, es gibt erwas, was die Ursache dieser Veränderung ist und was außerhalb der dritten Dimension liegt und Ausdruck der vierten Dimension ist. Was ist das?
Sehen Sie, wenn Sie diesen Würfel jetzt haben und ihn abzeichnen, so würden Sie sich vergeblich bemühen, wenn Sie ihn in verschiedenen Momenten anders zeichnen wollten; er wird immer derselbe bleiben. Wenn Sie die Pflanze abzeichnen, und Sie vergleichen nach drei Wochen das Bild mit Ihrem Modell, so hat es sich verändert. Diese Analogie stimmt also vollständig. Alles Lebende weist auf ein Höheres hin, worin es sein wahres Wesen hat, und der Ausdruck für dieses Höhere ist die Zeit. Die Zeit ist der symptomatische Ausdruck, die Erscheinung der Lebendigkeit [aufgefaßt als vierte Dimension] in den drei Dimensionen des physischen Raumes. Mit anderen Worten: Alle Wesen, für die die Zeit eine innere Bedeutung hat, sind Abbilder von vierdimensionalen Wesen. Dieser Würfel ist nach drei oder sechs Jahren immer noch derselbe. Der Lilienkeim ändert sich. Denn für ihn hat die Zeit eine reale Bedeutung. Daher ist das, was wir in der Lilie sehen, nur die dreidimensionale Abbildung des vierdimensionalen Lilienwesens. Die Zeit ist also ein Abbild, eine Projektion der vierten Dimension, der organischen Lebendigkeit, in die drei Raumdimensionen der physischen Welt.
Um sich klarzumachen, wie sich eine folgende Dimension zu der vorhergehenden verhält, bitte ich Sie, sich dieses zu denken: Der Würfel hat drei Dimensionen; wenn Sie sich die dritte vergegenwärtigen, so müssen Sie sich sagen, daß sie auf der zweiten senkrecht steht und die zweite senkrecht auf der ersten steht. Die drei Dimensionen zeichnen sich dadurch aus, daß sie senkrecht aufeinander stehen. Wir können uns aber noch eine andere Vorstellung machen, wie die dritte Dimension aus der folgenden [vierten Dimension] entsteht. Denken Sie sich, Sie würden den Würfel verändern, indem Sie die Grenzflächen farbig machen und diese Farben dann [in bestimmter Weise, wie bei Hinton] verändern. Eine solche Veränderung läßt sich in der Tat durchführen, und sie entspricht ganz genau der Veränderung, die ein dreidimensionales Wesen erleidet, wenn es in die vierte Dimension hinübergeht, sich durch die Zeit entwickelt. Wenn Sie ein vierdimensionales Wesen in irgendeinem Punkte durchschneiden, so heißt das, daß Sie ihm die vierte Dimension nehmen, sie vernichten. Wenn Sie das bei einer Pflanze tun, so machen Sie ganz genau dasselbe, als wenn Sie von der Pflanze einen Abdruck machen, einen Gipsabguß. Das haben Sie dadurch festgehalten, daß Sie die vierte Dimension, die Zeit, vernichteten. Dann bekommen Sie ein dreidimensionales Gebilde. Wenn bei irgendeinem dreidimensionalen Wesen die vierte Dimension, die Zeit, eine wesentliche Bedeutung hat, so handelt es sich um ein lebendiges Wesen.
Nun kommen wir in die fünfte Dimension hinein. Da können Sie sich sagen, Sie müssen wiederum eine Grenze haben, die senkrecht auf der vierten Dimension steht. Von der vierten Dimension haben wir gesehen, daß sie in ähnlicher Beziehung zur dritten Dimension steht, wie die dritte zur zweiten. Von der fünften kann man sich nicht gleich ein solches Bild machen. Aber eine ungefähre Vorstellung können Sie sich wieder durch eine Analogie schaffen. Wie entsteht überhaupt eine Dimension? Wenn Sie einfach eine Linie ziehen, wird niemals eine weitere Dimension entstehen, wenn Sie die Linie nur in einer Richtung fortschieben würden. Erst durch die Vorstellung, daß Sie zwei einander entgegenkommende Kräfterichtungen haben, die sich dann in einem Punkte stauen, erst durch den Ausdruck der Stauung haben Sie eine neue Dimension. Wir müssen also die neue Dimension als eine neue Stauungslinie [zweier Kräfteströmungen] auffassen können, und uns die eine Dimension das eine Mal von rechts, das andere Mal von links kommend denken, als positiv und negativ. Ich fasse also eine Dimension [als in sich] polaren [Kräftestrom] auf, so daß sie eine positive und eine negative Dimension[skomponente] hat, und die Neutralisation [dieser polaren Kräftekomponenten], das ist die neue Dimension.
Von da ausgehend wollen wir uns eine Vorstellung von der fünften Dimension schaffen. Da werden wir uns vorzustellen haben, daß die vierte Dimension, die wir als Zeit ausgedrückt gefunden haben, sich in positiver und negativer Weise verhält. Nehmen Sie nun zwei Wesen, für die die Zeit eine Bedeutung hat, und denken Sie sich zwei solche Wesen miteinander in Kollision geraten. Dann muß etwas als Ergebnis erscheinen, ähnlich wie wir früher von einer Stauung von [entgegengesetzten] Kräften geredet haben; und was da als Resultat auftritt, wenn zwei vierdimensionale Wesen miteinander in Beziehung treten, das ist ihre fünfte Dimension. Diese fünfte Dimension ergibt sich als Resultat, als Folge eines Austausches [einer Neutralisation polarer Kräftewirkungen], indem zwei Lebewesen durch ihr gegenseitiges Aufeinanderwirken etwas hervorbringen, was sie nicht außen [in den drei gewöhnlichen Raumdimensionen miteinander gemeinsam] haben, auch nicht in [der vierten Dimension,] der Zeit, gemeinsam haben, sondern völlig außerhalb dieser [bisher besprochenen Dimensionen oder] Grenzen haben. Das ist das, was wir Mitgefühl [oder Empfindung] nennen, wodurch ein Wesen von dem andern weiß, also die Erkenntnis des [seelisch-geistigen] Innern eines anderen Wesens. Niemals könnte ein Wesen von dem anderen Wesen etwas wissen außerhalb der Zeit [und des Raumes], wenn Sie nicht noch eine höhere, fünfte Dimension hinzufügten, [also in die Welt der] Empfindung [einträten]. Natürlich ist hier die Empfindung nur als Projektion, als Ausdruck [der fünften Dimension] in der physischen Welt [zu verstehen].
Die sechste Dimension in derselben Weise zu entwickeln, würde zu schwer werden, daher will ich sie nur angeben. [Versuchten wir so fortzuschreiten, so würde sich als Ausdruck der sechsten Dimension etwas entwickeln lassen, das,] in die dreidimensionale physische Welt hereingelegt, Selbstbewußtsein ist.
Der Mensch ist als dreidimensionales Wesen ein solches, das mit den anderen dreidimensionalen Wesen seine Bildlichkeit gemeinschaftlich hat. Die Pflanze hat dazu noch die vierte Dimension. Aus diesem Grunde werden Sie auch niemals das letzte [eigentliche] Wesen der Pflanze innerhalb der drei Dimensionen des Raumes finden, sondern Sie müßten von der Pflanze aufsteigen zu einer vierten Raumdimension [zur Astralsphäre]. Wollten Sie aber gar ein Wesen begreifen, das Empfindung hat, so müßten Sie zur fünften Dimension [zum unteren Devachan, zur RupaSphäre] aufsteigen; und wollten Sie ein Wesen begreifen, das Selbstbewußtsein hat, einen Menschen, so müßten Sie bis zur sechsten Dimension [zum oberen Devachan, zur Arupa-Sphäre] aufsteigen. So ist der Mensch, wie er gegenwärtig vor uns steht, in der Tat ein sechsdimensionales Wesen. Dasjenige, was hier Empfindung oder Mitgefühl, beziehungsweise Selbstbewußtsein genannt wird, ist eine Projektion der fünften, beziehungsweise sechsten Dimension in den gewöhnlichen dreidimensionalen Raum. In diese geistigen Sphären ragt der Mensch, wenn auch in der Hauptsache unbewußt, hinein; erst dort kann er tatsächlich in dem letztangedeuteten Sinne erlebt werden. Dieses sechsdimensionale Wesen kann nur dadurch zu einer Vorstellung selbst der höheren Welten kommen, wenn es versucht, sich des eigentlich Charakteristischen der niederen Dimensionen zu entledigen.
Nur andeuten kann ich Ihnen den Grund, warum der Mensch die Welt für nur dreidimensional hält, weil er nämlich in seiner Vorstellung eben darauf angelegt ist, in der Welt nur ein Spiegelbild von Höherem zu sehen. Vor einem Spiegel sehen Sie auch nur ein Spiegelbild von sich selbst. So sind in der Tat die drei Dimensionen unseres physischen Raumes Spiegelungen, materielle Abbilder von drei höheren, ursächlich schöpferischen Dimensionen. Unsere materielle Welt hat demnach ihr polares [geistiges] Gegenbild in der Gruppe der drei nächsthöheren Dimensionen, also in denen der vierten, fünften und sechsten Dimension. Und in ähnlichem Sinne verhalten sich auch die jenseits dieser Gruppe von Dimensionen liegenden, nur zu ahnenden geistigen Welten, polar zu denen der vierten bis sechsten Dimension.
Wenn Sie Wasser haben, und Sie lassen das Wasser gefrieren, so ist in beiden Fällen dieselbe Substanz da; in der Form aber unterscheiden sie sich ganz wesentlich. Einen ähnlichen Prozeß können Sie sich für die drei höheren Dimensionen des Menschen vorstellen. Wenn Sie sich den Menschen als bloß geistiges Wesen denken, dann müssen Sie sich denken, daß er nur die drei höheren Dimensionen — Selbstbewußtsein, Gefühl und Zeit — hat, und diese drei Dimensionen spiegeln sich in der physischen Welt in deren drei gewöhnlichen Dimensionen.
Der Yogi [Geheimschüler] muß, wenn er zu einer Erkenntnis der höheren Welten aufrücken will, die Spiegelbilder nach und nach durch die Wirklichkeit ersetzen. Wenn er zum Beispiel eine Pflanze betrachtet, so muß er sich daran gewöhnen, eben die höheren Dimensionen allmählich anstelle der niederen zu setzen. Betrachtet er eine Pflanze, und ist er imstande, bei einer Pflanze von einer Raumdimension abzusehen, von einer Raumdimension zu abstrahieren, und sich dafür zunächst einmal eine entsprechende der höheren Dimensionen vorzustellen, also die Zeit, dann erhält er tatsächlich eine Vorstellung davon, was ein zweidimensionales, in Bewegung begriffenes Wesen ist. Damit dieses Wesen nicht nur ein bloßes Bild ist, sondern etwas, was einer Wirklichkeit entspricht, muß der Yogi noch folgendes machen. Wenn er nämlich von der dritten Dimension absieht und die vierte hinzufügt, so würde er nur etwas Imaginäres erhalten. Durch folgende Hilfsvorstellung [kann man sich aber weiterhelfen]: Wenn wir uns von einem lebenden Wesen eine kinematographische Darstellung machen, so nehmen wir den ursprünglich dreidimensionalen Vorgängen die dritte Dimension weg, fügen aber durch die Szenenfolge der Bilder die [Dimension der] Zeit hinzu. Wenn wir dann zu dieser [bewegten] Vorstellung noch die Empfindung hinzufügen, so vollziehen wir eine ähnliche Prozedur, wie ich sie Ihnen früher als Abkrümmen eines dreidimensionalen Gebildes in die vierte Dimension hinein beschrieben habe. Durch diesen Prozeß bekommen Sie dann ein vierdimensionales Gebilde, jetzt aber ein solches, das zwei von unseren Raumdimensionen hat, aber außerdem noch zwei höhere, nämlich Zeit und Empfindung. Solche Wesen gibt es in der Tat, und diese Wesen - und damit komme ich zu einem realen Schluß der ganzen Betrachtung —, diese Wesen möchte ich Ihnen nennen.
Denken Sie sich zwei Raumdimensionen, also eine Fläche, und diese Fläche begabt mit Bewegung. Nun denken Sie sich abgebogen als Empfindung ein empfindendes Wesen, das dann eine zweidimensionale Fläche vor sich herschiebt. Ein solches Wesen muß anders wirken und sich sehr unterscheiden von einem dreidimensionalen Wesen unseres Raumes. Dieses Flächenwesen, das wir uns auf diese Weise konstruiert haben, ist nach einer Richtung unabgeschlossen, völlig offen, es bietet Ihnen einen zweidimensionalen Anblick; Sie können nicht um es herum, es kommt auf Sie zu. Das ist ein Leuchtwesen, und das Leuchtwesen ist nichts anderes als die Unabgeschlossenheit nach einer Richtung.
Durch ein solches Wesen lernen die Eingeweihten dann andere Wesen kennen, die sie beschreiben als die göttlichen Boten, die ihnen in Feuerflammen nahen. Die Beschreibung vom Sinai, als dem Moses die zehn Gebote gegeben worden sind,® heißt nichts anderes, als daß sich ihm in der Tat ein Wesen nähern konnte, das für ihn wahrnehmbar diese Abmessungen hatte. Es wirkte auf ihn wie ein Mensch, dem man die dritte Raumdimension fortgenommen hatte, es wirkte in der Empfindung und in der Zeit.
Diese abstrakten Bilder in den religiösen Urkunden sind nicht nur äußere Sinnbilder, sondern gewaltige Wirklichkeiten, die der Mensch kennenlernen kann, wenn er das sich anzueignen imstande ist, was wir durch Analogien uns klarzumachen versuchten. Je mehr Sie sich solchen Betrachtungen von Analogien fleißig und energisch hingeben, emsig sich hineinvertiefen, desto mehr wirken Sie wirklich auf Ihren Geist, und um so mehr wirken diese [Betrachtungen] in uns und lösen höhere Fähigkeiten aus. [Dies ist etwa der Fall bei der Auseinandersetzung mit] der Analogie des Verhältnisses des Würfels zum Sechseck und des Tessarakts zum Rhombendodekaeder. Letzteres stellt eine Projektion des Tessaraktes in die dreidimensionale physische Welt dar. Wenn Sie sich diese Figuren als für sich lebend veranschaulichen, wenn Sie aus der Projektion des Würfels — dem Sechseck — den Würfel herauswachsen lassen, und ebenso aus der Projektion des Tessaraktes [dem Rhombendodekaeder] den Tessarakt selbst enstehen lassen, dann schaffen Sie sich dadurch in Ihrem niederen Mentalkörper die Möglichkeit und die Fähigkeit, das aufzufassen, was ich Ihnen eben als Gebilde beschrieben habe. Und wenn Sie, mit anderen Worten, nicht nur mir gefolgt sind, sondern diese Prozedur lebendig durchgemacht haben, wie der Yogi beim wachen Bewußtsein, dann werden Sie merken, daß Ihnen in Ihren Träumen so etwas auftreten wird, das in Wirklichkeit ein vierdimensionales Gebilde ist, und dann ist es nicht mehr weit, es herüberzuholen in das wache Bewußtsein, und Sie können dann bei jedem vierdimensionalen Wesen die vierte Dimension sehen.
Die astrale Sphäre ist die vierte Dimension. Devachan bis Rupa ist die fünfte Dimension. Devachan bis Arupa ist die sechste Dimension.
Diese drei Welten, die physische, astralische und himmlische [devachanische], umschließen sechs Dimensionen. Die noch höheren Welten verhalten sich vollständig polar zu diesen.
Mineral Pflanze Tier Mensch Arupa Selbstbewußtsein Rupa Empfindung Selbstbewußtsein Astralplan Leben Empfindung Selbstbewußtsein Physischer Form Leben Empfindung SelbstPlan bewußtsein Form Leben Empfindung Form Leben Form

