The Fourth Dimension
GA 324a
7 November 1905, Berlin
Translated by Steiner Online Library
Four-dimensional Space
Our ordinary space has three dimensions: length, width and height. A line extends in one dimension, it has only length. A table is a surface, so it has two dimensions: length and width. A body extends in three dimensions. How does a body of three dimensions come about?
Imagine a shape that has no dimensionality at all: that is the point. It has zero dimensions. When a point moves in one direction, a straight line is created, a one-dimensional shape. If you imagine the line continuing, a surface with length and width is created. Finally, if you imagine the surface moving, it describes a three-dimensional shape. But we cannot use the same method to create a fourth dimension from a three-dimensional object [through movement]. We must try to visualize how we can arrive at the concept of a fourth dimension. [Certain] mathematicians [and natural scientists] have felt compelled to harmonize the spiritual world with our sensual world [by placing the spiritual world in a four-dimensional space], for example, Zöllner.
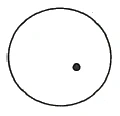
Imagine a circle. It is closed on all sides in the plane. If someone demands that a coin should come into the circle from outside, we have to cross the circle line (Figure 46). But if you do not want to touch the circle line, you have to lift the coin [into the space] and then put it in. You must necessarily go from the second to the third dimension. If we wanted to conjure a coin into a cube [or into a sphere], we would have to go [out of the third dimension and] through the fourth dimension.'
In this life, the first time I began to grasp what space actually is was when I started to study recent [synthetic projective] geometry. Then I realized what it means to go from a circle to a line (Figure 47). In the most intimate thinking of the soul, the world opens up.
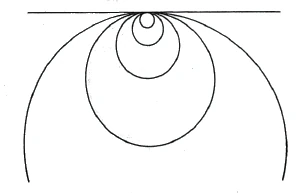
Now let us imagine a circle. If we follow the circle line, we can walk around it and return to the original point. Now let us imagine the circle getting bigger and bigger [holding a tangent line]. In the end, it must merge into a straight line because it flattens out more and more. [When I go through the enlarging circles, I always go down on one side and then come up on the other side and back to the starting point. If I finally move on the straight line, for example to the right into infinity, I have to return from the other side of infinity, since the straight line behaves like a circle in terms of the arrangement of its points. From this we see that space has no end [in the same sense that the straight line has no end, that is, the arrangement of its points is the same as in a closed circle. Accordingly, we must think of infinitely extended space as closed in itself, just as the surface of a sphere is closed in itself]. Thus you have represented infinite space [in the sense of] a circle [or] a sphere. This concept leads us to imagine space in its reality.
If I now imagine that I do not simply disappear [into infinity] and then return [unchanged from the other side], but think to myself that I have a radiating light, this will become weaker and weaker as I move away (seen from a stationary point on the line) and stronger and stronger when I return (with the light from infinity). And if we consider that this light not only has a positive effect, but, as it approaches from the other side here, shines all the more strongly, then you have [here the qualities] positive and negative.
In all natural effects, you will find these two poles, which represent nothing other than the opposite effects of space. From this you get the idea that space is something powerful, and that the forces that work in it are nothing other than the outflow of the power itself. Then we will have no doubt that within our three-dimensional space there could be a force that works from within. You will realize that everything that occurs in space is based on real relationships in space.
If we were to intertwine two dimensions, we would have brought these two into relation. If you want to entwine two [closed] rings, you have to unravel one of them to get the other inside. But now I will demonstrate the inner diversity of space by entwining this structure [a rectangular paper band] twice around itself [that is, holding one end and twisting the other end 360° and then holding the two ends together]. I pin the paper tape together tightly with pins and cut it in half. Now one tape is firmly stuck inside the other. Before that, it was just one tape. So here, by merely intertwining the tapes within the three dimensions, I have created the same thing that I would otherwise have to reach out into the [fourth] dimension to achieve."
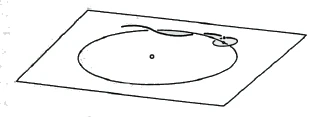
This is not a gimmick, but reality. If we have the sun here, and the earth's orbit around the sun here, and the moon's orbit around the earth here (Figure 48), we have to imagine that the earth moves around the sun and therefore the moon's orbit and the earth's orbit are intertwined exactly [like our two paper ribbons]. Now the moon has branched off from the earth [in the course of the earth's development]. This is an internal bifurcation that has occurred in the same way [as the intertwining of our two paper ribbons]. [Through such a way of looking at it] space comes alive in itself.
Now consider a square. Imagine it moving through space in such a way that it forms a cube. Then it must progress within itself.
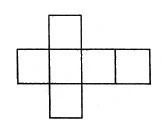
A cube is composed of six squares, which together form the surface of the cube. To put the cube together [in a clear way], I first place the six squares next to each other [in a plane] (Figure 49). I get the cube again when I put these squares on top of each other. I then have to place the sixth on top by going through the third dimension. Thus I have now laid the cube out in two dimensions. I have transformed a three-dimensional structure by laying it out in two dimensions.
Now imagine that the boundaries of a cube are squares. If I have a three-dimensional cube here, it is bounded by two-dimensional squares. Let's just take a single square. It is two-dimensional and is bounded by four one-dimensional lines. I can expand the four lines into a single dimension (Figure 50). What appears in the one dimension, I will now paint in red [solid line] and the other dimension in blue [dotted line]. Now, instead of saying length and width, I can speak of the red and blue dimensions.

I can reassemble the cube from six squares. So now I go from the number four [the number of side lines of the square] to the number six [the number of the side surfaces of the cube]. If I go one step further, I get from the number six [the number of the side surfaces of the cube] to the number eight [the number of “side cubes” of a four-dimensional structure]. I now arrange the eight cubes in such a way that the corresponding structure is created in three-dimensional space to that which was previously constructed in two-dimensional space (Figure 51) from six squares.
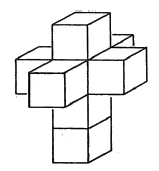
Imagine that I could turn this structure inside out so that I could turn it right way up and put it together in such a way that I could cover the whole structure with the eighth cube. Then I would get a four-dimensional structure in a four-dimensional space from the eight cubes. This figure is called [by Hinton] the tessaract. Its limiting figure is eight cubes, just as the ordinary cube has six squares as its limiting figure. The [four-dimensional] tessaract is therefore bounded by [eight] three-dimensional cubes.
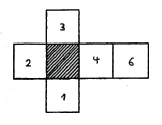
Imagine a creature that can only see in two dimensions, and this creature would now look at the squares laid out separately, it would only see the squares 1, 2, 3, 4 and 6, but never the hatched square 5 in the middle (Figure 52). It is quite the same for you with the four-dimensional structure. [Since you can only see three-dimensional objects, you] cannot see the hidden cube in the middle.
Now imagine the cube drawn on the board like this [so that the outline forms a regular hexagon]. The other side is hidden behind it. This is a kind of silhouette, a projection of the cube into two-dimensional space (Figure 53). This two-dimensional silhouette of a three-dimensional cube consists of rhombi, oblique rectangles [parallelograms]. If you imagine the cube made of wire, you would also be able to see the rhomboid squares at the back. So here you have six interlocking rhomboid squares in the projection. In this way you can project the whole cube into two-dimensional space.
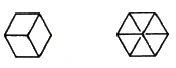
Now imagine our tetrahedron formed in four-dimensional space. If you project this figure into three-dimensional space, you should get four non-intersecting rhombic parallelpipeds. One of these rhombic parallelpipeds should be drawn as follows (Figure 54).
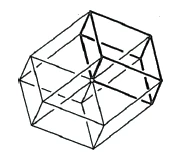
Eight such shifted rhombic cubes would have to be inserted into each other in order to obtain a three-dimensional image of the four-dimensional tessaract in three-dimensional space. Thus, we can represent the three-dimensional shadow image of such a tessaract with the help of eight rhombic cubes that are suitably inserted into each other. The spatial structure that results is a rhombic dodecahedron with four spatial diagonals (Figure 55). Just as in the rhombus representation of the cube, three directly neighboring rhombuses are shifted into each other, so that only three of the six cube surfaces are seen in the projection, only four non-intersecting rhombic cubes appear in the rhombic dodecahedron only four non-intersecting rhombic cubes appear as projections of the eight boundary cubes, since four of the directly neighboring rhombic cubes completely cover the remaining four.'>
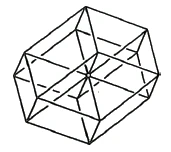
We can construct the three-dimensional shadow of a four-dimensional body, but not the tessaract itself. In the same sense, we are the shadows of four-dimensional beings. Thus, as man rises from the physical to the astral, he must develop his powers of visualization. Let us imagine a two-dimensional being who makes an [intense and repeated] effort to vividly imagine such a [three-dimensional] shadow image. When it then surrenders to the dream, then (...).
When you mentally build up the relationship between the third and fourth dimensions, the forces at work within you allow you to see into [real, not mathematical] four-dimensional space.
We will always be powerless in the higher world if we do not acquire the abilities [to see in the higher world] here [in the world of ordinary consciousness]. Just as a person in the womb develops eyes to see in the physical-sensual world, so must a person in the womb of the earth develop [supernatural] organs, then he will be born in the higher world [as a seer]. The development of the eyes in the womb is an [illuminating] example [of this process].
The cube would have to be constructed from the dimensions of length, width and height. The tessaract would have to be constructed from the dimensions of length, width, height and a fourth dimension.
As the plant grows, it breaks through three-dimensional space. Every being that lives in time breaks through the three [ordinary] dimensions. Time is the fourth dimension. It is invisibly contained in the three dimensions of ordinary space. However, you can only perceive it through clairvoyant power.
A moving point creates a line; when a line moves, a surface is created; and when a surface moves, a three-dimensional body is created. If we now let the three-dimensional space move, we have growth [and development]. This gives you four-dimensional space, time [projected into three-dimensional space as movement, growth, development].
[The geometric consideration of the structure of the three ordinary dimensions] can be found in real life. Time is perpendicular to the three dimensions, it is the fourth, and it grows. When you bring time to life within you, sensation arises. If you increase the time within you, move it within yourself, you have the sentient animal being, which in truth has five dimensions. The human being actually has six dimensions.
We have four dimensions in the etheric realm [astral plane], five dimensions in the astral realm [lower devachan] and six dimensions in the [upper] devachan.
Thus the [spiritual] manifoldness swells up to you. The devachan, as a shadow cast into the astral realm, gives us the astral body; the astral realm, as a shadow cast into the etheric realm, gives us the etheric body, and so on.
Time flows in one direction, which is the withering away of nature, and in the other direction it is the revival. The two points where they merge are birth and death.
The future is constantly coming towards us. If life only went in one direction, nothing new would ever come into being. Man also has genius – that is his future, his intuitions, which flow towards him. The processed past is [the stream coming from the other side; it determines] the essence [of how it has become so far].
Der Vierdimensionale Raum
Unser gewöhnlicher Raum hat drei Dimensionen: Länge, Breite und Höhe. Eine Linie ist in einer Dimension ausgedehnt, sie hat nur Länge. Die Tafel ist eine Fläche, hat also zwei Dimensionen: Länge und Breite. Ein Körper dehnt sich nach drei Dimensionen aus. Wie entsteht nun ein Körper aus drei Dimensionen?
Stellen Sie sich ein Gebilde vor, das gar keine Dimensionalität hat, das ist der Punkt. Er hat null Dimensionen. Wenn ein Punkt sich bewegt und eine Richtung einhält, so entsteht eine gerade Linie, ein eindimensionales Gebilde. Wenn Sie sich die Linie weiterbewegt denken, so entsteht eine Fläche mit Länge und Breite. Wenn Sie schließlich die Fläche sich bewegt denken, so beschreibt sie ein dreidimensionales Gebilde. Auf diesselbe Weise können wir aber nicht mehr aus dem dreidimensionalen Körper [durch Bewegung] ein vierdimensionales Gebilde, eine vierte Dimension erzeugen. Wir müssen versuchen, uns bildlich vorzustellen, wie wir zum Begriff einer vierten Dimension kommen können. [Gewisse] Mathematiker [und Naturwissenschaftler] haben sich versucht gefühlt, die geistige Welt mit unserer sinnlichen Welt in Einklang zu bringen [, indem sie die geistige Welt in einen vierdimensionalen Raum hineinversetzten], so zum Beispiel Zöllner.”

Denken Sie sich einen Kreis. Er ist nach allen Seiten hin in der Ebene geschlossen. Wenn jemand verlangt, daß eine Münze von außerhalb des Kreises in den Kreis hineinkommen soll, müssen wir die Kreislinie überschreiten (Figur 46). Falls Sie aber die Kreislinie nicht berühren wollen, so müssen Sie die Münze [in den Raum] heben und dann hineinlegen. Sie müssen dabei notwendigerweise aus der zweiten in die dritte Dimension gehen. Falls wir eine Münze in einen Würfel [oder in eine Kugel] hineinzaubern wollten, so müßten wir [aus der dritten Dimension heraus und] durch die vierte Dimension hindurchgehen.’
Als ich in diesem Leben zu erfassen anfıng, was der Raum eigentlich ist, war es, als ich anfing, neuere [synthetische projektive] Geometrie zu studieren. Da begriff ich, was es für eine Bedeutung hat, wenn man von einem Kreise in eine Linie übergeht (Figur 47). Im intimsten Denken der Seele eröffnet sich die Welt.”

Denken wir uns nun einen Kreis. Wenn wir die Kreislinie verfolgen, können wir auf ihr herum gehen und zu dem ursprünglichen Punkte zurückkehren. Denken wir uns nun den Kreis immer größer und größer werdend [wobei wir eine Tangentenlinie festhalten]. Dabei muß er zuletzt in eine gerade Linie übergehen, da er sich immer mehr verflacht. [Wenn ich die sich vergrößernden Kreise durchlaufe, so gehe ich immer auf der einen Seite] hinunter [und komme dann auf der anderen Seite wieder] herauf und zurück zum Ausgangspunkt. [Bewege ich mich schließlich auf der geraden Linie etwa nach rechts bis ins Unendliche, so] muß ich von der anderen [linken] Seite von der Unendlichkeit wieder zurückkehren, da die gerade Linie sich [bezüglich der Anordnung ihrer Punkte] wie ein Kreis verhält. Daraus sehen wir, daß der Raum keinen Abschluß hat [im selben Sinne, wie die gerade Linie keinen Abschluß hat, das heißt, die Anordnung ihrer Punkte ist dieselbe wie bei einem in sich geschlossenen Kreis. Entsprechend muß man sich den unendlich ausgedehnten Raum als in sich geschlossen denken, so wie die Oberfläche einer Kugel in sich geschlossen ist]. Damit haben Sie den unendlichen Raum dargestellt [im Sinne] eines Kreises, [oder] einer Kugel. Dieser Begriff führt uns dazu, den Raum vorzustellen in seiner Wirklichkeit.
Wenn ich mir nun vorstelle, daß ich nicht einfach wesenlos [ins Unendliche] fortgehe, um dann [unverändert von der anderen Seite] zurückzukehren, sondern mir denke, ich habe hier ein ausstrahlendes Licht, so wird dieses [von einem ruhenden Punkt auf der Linie aus gesehen] immer schwächer, indem ich [mit dem Licht] fortgehe, und immer stärker, wenn ich [aus dem Unendlichen mit dem Licht wieder] zurückkehre. Und denken wir, daß dieses Licht nicht nur positiv wirkt, sondern, indem es hier sich [wieder] nähert von der anderen Seite, desto stärker leuchtet, so haben Sie [hier die Qualitäten] positiv und negativ.
Bei allen Naturwirkungen finden Sie diese zwei Pole, die nichts anderes darstellen, als die entgegengesetzten Wirkungen des Raumes. Daraus bekommen Sie den Begriff, daß der Raum etwas Kraftvolles ist, und daß die Kräfte, die darin wirken, nichts anderes sind als der Ausfluß der Kraft selbst. Dann werden wir nicht zweifeln können, daß sich innerhalb unseres dreidimensionalen Raumes eine Kraft finden könnte, die von innen wirkt. Sie werden sich klar werden, daß alles, was im Raume auftritt, auf wirklichen Verhältnissen im Raume beruht.
Denken wir zwei Dimensionen miteinander verschlungen, dann hätten wir diese zwei in Beziehung gebracht. Wenn Sie zwei [geschlossene] Ringe miteinander verschlingen wollen, müssen Sie den einen aufdröseln, um den anderen hineinzubringen. Ich werde mir nun aber die innere Mannigfaltigkeit des Raumes bezeugen, indem ich dieses Gebilde [ein rechteckiges Papierband] zweimal um sich selbst verschlinge [das heißt, das eine Ende festhalte und das andere Ende um 360° verdrehe und dann die beiden Enden zusammenhalte]. Ich hefte das Papierband fest mit Stecknadeln zusammen und zerschneide es in der Mitte. Jetzt hängt das eine Band ganz fest in dem anderen drinnen. Vorher war es nur ein Band. Ich habe also hier durch bloße Bandverschlingungen innerhalb der drei Dimensionen dasselbe erzeugt, was ich sonst [nur] durch Hinausgehen in die [vierte] Dimension erreichen kann.“
So etwas ist keine Spielerei, sondern Wirklichkeit. Wenn wir hier die Sonne haben, und hier die Erdbahn um die Sonne, und hier die Mondbahn um die Erde (Figur 48), so müssen wir uns vorstellen, daß sich die Erde um die Sonne bewegt und deshalb die Mondbahn und die Erdbahn genauso verschlungen sind [wie unsere zwei Papierbänder]. Nun hat sich der Mond [im Laufe der Erdenentwicklung] von der Erde abgezweigt. Das ist eine innere Abzweigung, die auf dieselbe Art vor sich gegangen ist [wie die Verschlingung unserer zwei Papierbänder zustande gekommen ist]. [Durch eine solche Betrachtungsweise] wird der Raum in sich lebendig.

Betrachten Sie nun ein Quadrat. Denken Sie es sich so [durch den Raum] bewegt, daß es einen Würfel bildet. Dann muß es in sich selbst vorwärtsschreiten.
Ein Würfel ist aus sechs Quadraten zusammengesetzt, sie bilden zusammen die Oberfläche des Würfels. Um den Würfel [in übersichtlicher Weise] zusammenzufügen, lege ich die sechs Quadrate zunächst nebeneinander [in eine Ebene] (Figur 49). Ich kriege den Würfel wieder, wenn ich diese Quadrate aufstülpe. Das sechste muß ich dann oben drauf legen, indem ich durch die dritte Dimension hindurchgehe. Dadurch habe ich nun den Würfel auseinandergelegt in zwei Dimensionen. Ich habe verwandelt ein dreidimensionales Gebilde durch Auseinanderlegen in ein zweidimensionales.

Denken Sie sich nun, daß die Grenzen eines Würfels Quadrate sind. Habe ich hier einen dreidimensionalen Würfel, so ist er begrenzt von zweidimensionalen Quadraten. Nehmen wir einmal bloß ein einziges Quadrat. Es ist zweidimensional und wird begrenzt von vier eindimensionalen Linien. Ich kann die vier Linien in eine einzige Dimension ausbreiten (Figur 50). Was in der einen Dimension erscheint, werde ich nun rot [ausgezogene Linie] malen und die andere Dimension blau [punktierte Linie] streichen. Jetzt kann ich, statt Länge und Breite zu sagen, von der roten und der blauen Dimension sprechen.

Aus sechs Quadraten kann ich den Würfel wieder zusammensetzen. Ich gehe also jetzt über von der Zahl vier [der Anzahl der Seitenlinien des Quadrates] zur Zahl sechs [der Anzahl der Seitenflächen des Würfels]. Gehe ich noch einen Schritt weiter, so komme ich von der Zahl sechs [der Anzahl der Seitenflächen des Würfels] zur Zahl acht [der Anzahl «Seitenwürfel» eines vierdimensionalen Gebildes]. Ich ordne nun die acht Würfel so an, daß dadurch im dreidimensionalen Raume das entsprechende Gebilde entsteht zu dem früher [aus sechs Quadraten aufgebauten Gebilde] in der zweidimensionalen Fläche (Figur 51).

Denken Sie sich, ich würde imstande sein, dieses Gebilde so umzustülpen, daß ich es richtig aufdrehe und so zusammenfüge, daß ich mit dem achten Würfel das ganze Gebilde zudecke, dann kriege ich aus den acht Würfeln ein vierdimensionales Gebilde in einem vierdimensionalen Raum. Dieses Gebilde heißt [nach Hinton] das Tessarakt. Es hat als sein Grenzgebilde acht Würfel, ganz entsprechend wie der gewöhnliche Würfel als sein Grenzgebilde sechs Quadrate hat. Das [vierdimensionale] Tessarakt ist also von [acht] dreidimensionalen Würfeln begrenzt.
Denken Sie sich ein Wesen, das nur in zwei Dimensionen sehen kann, und dieses Wesen würde nun die auseinandergelegten Quadrate anschauen, es würde nur die Quadrate 1, 2, 3, 4 und 6 sehen, nie aber das schraffierte Quadrat 5 in der Mitte (Figur 52). Ganz entsprechend geht es Ihnen mit dem vierdimensionalen Gebilde. [Da Sie nur dreidimensionale Objekte sehen können, so] können Sie den verborgenen Würfel in der Mitte nicht sehen.

Denken Sie sich nun den Würfel so auf die Tafel gezeichnet [so daß als Umriß ein regelmäßiges Sechseck entsteht]. Das andere ist hinten verborgen. Dies ist eine Art Schattenbild, eine Projektion des Würfels in den zweidimensionalen Raum (Figur 53). Dieses zweidimensionale Schattenbild eines dreidimensionalen Würfels besteht aus Rhomben, aus schiefen Vierecken [Parallelogramme]. Denken Sie sich den Würfel aus Draht hergestellt, so würden Sie auch die hinteren Rhomben-Vierecke sehen können. Sie haben hier also in der Projektion sechs ineinandergeschobene RhombenVierecke. Auf diese Weise können Sie den ganzen Würfel hineinwerfen in den zweidimensionalen Raum.
Denken Sie sich nun unser Tessarakt gebildet im vierdimensionalen Raum. Wenn Sie dieses Gebilde in den dreidimensionalen Raum hineinwerfen, so müssen Sie vier [sich gegenseitig nicht durchdringende rhombisch] verschobene schiefe Würfel [Parallelepipede] kriegen. Einer dieser rhombisch verschobenen Würfel müßte so gezeichnet werden (Figur 54).

Acht solche verschobenen Rhomben-Würfel müßten [aber] ineinandergesteckt werden, damit man im dreidimensionalen Raum [ein vollständiges] dreidimensionales Bild des vierdimensionalen Tessaraktes erhält. Damit können wir also das [vollständige] dreidimensionale Schattenbild eines solchen Tessaraktes darstellen mit Hilfe von acht [geeignet] ineinander geschobenen Rhomben-Würfeln. [Als Raumgebilde ergibt sich dabei ein Rhombendodekaeder mit vier Raumdiagonalen (Figur 55). So wie bei der RhombenDarstellung des Würfels je drei unmittelbar benachtbarte Rhomben gegenseitig verschoben ineinander zu liegen kommen, man also von den sechs Würfelflächen nur drei in der Projektion sieht, so erscheinen auch bei der Rhombendodekaeder-Darstellung des Tessaraktes nur vier sich nicht gegenseitig durchdringende Rhomben-Würfel als Projektionen der acht Grenz-Würfel, da je vier der unmittelbar benachbarten Rhomben-Würfel die übrigen vier vollkommen überdecken.‘]

Den dreidimensionalen Schatten eines vierdimensionalen Körpers können wir also konstruieren, wenn auch nicht das Tessarakt selbst. Im selben Sinne sind wir der Schatten von vierdimensionalen Wesen. So muß der Mensch, wenn er vom Physischen zum Astralen steigt, sein Vorstellungsvermögen ausbilden. Denken wir uns ein zweidimensionales Wesen, das sich [intensiv und wiederholt] bemüht, ein solches [dreidimensionales] Schattenbild recht lebhaft vorzustellen. Wenn es sich dann dem Traum überläßt, so quellen dann (...).
Wenn Sie sich aufbauen im Geiste das Verhältnis der dritten zur vierten Dimension, so arbeiten in Ihnen die Kräfte, die Sie in den [wirklichen, nicht den mathematischen] vierdimensionalen Raum hineinschauen lassen.
Wir werden immer ohnmächtig sein in der höheren Welt, wenn wir uns nicht hier [in der Welt des gewöhnlichen Bewußtseins] die Fähigkeiten [des Sehens in der höheren Welt] erwerben werden. So wie der Mensch im Mutterleib die Augen zum Sehen in der physisch-sinnlichen Welt ausbildet, so muß der Mensch im Mutterleib der Erde [übersinnliche] Organe ausbilden, dann wird er in der höheren Welt [als Sehender] geboren. Die Ausbildung der Augen im Mutterleib ist ein [erhellendes] Beispiel [für diesen Prozeß].
Der Würfel müßte aus den Dimensionen Länge, Breite und Höhe aufgebaut werden. Das Tessarakt müßte ich aufbauen aus den Dimensionen Länge, Breite, Höhe und einer vierten Dimension.
Indem die Pflanze wächst, durchbricht sie den dreidimensionalen Raum. Jedes Wesen, das in der Zeit lebt, durchbricht die drei [gewöhnlichen] Dimensionen. Die Zeit ist die vierte Dimension. Sie steckt unsichtbar in den drei Dimensionen des gewöhnlichen Raumes darinnen. Sie können sie aber nur durch hellseherische Kraft wahrnehmen.
Ein bewegter Punkt erzeugt eine Linie; bewegt sich eine Linie, so entsteht eine Fläche; und bewegt sich ein Fläche, so ensteht der dreidimensionale Körper. Lassen wir nun den dreidimensionalen Raum sich bewegen, so haben wir Wachstum [und Entwicklung]. Sie haben dadurch den vierdimensionalen Raum, die Zeit [hineinprojiziert in den dreidimensionalen Raum als Bewegung, Wachstum, Entwicklung].
[Die geometrische Betrachtung zum Aufbau der drei gewöhnlichen Dimensionen] finden Sie fortgesetzt im wirklichen Leben. Die Zeit steht senkrecht auf den drei Dimensionen, sie ist die vierte, sie wächst. Wenn Sie die Zeit in sich lebendig machen, entsteht die Empfindung. Vermehren Sie die Zeit in sich, bewegen Sie sie in sich selbst, so haben Sie das empfindende Tierwesen, das in Wahrheit fünf Dimensionen hat. Das Menschenwesen hat in Wahrheit sechs Dimensionen.
Wir haben vier Dimensionen im Ätherbereich [Astralplan], fünf Dimensionen im Astralbereich [unteres Devachan] und sechs Dimensionen im [oberen] Devachan.
So quellen Ihnen die [geistigen] Mannigfaltigkeiten auf. Das Devachan als Schatten in den Astralraum geworfen, gibt uns den Astralkörper, der Astralraum als Schatten in den Ätherraum geworfen, gibt uns den Ätherkörper, und so weiter.
Die Zeit geht nach einer Seite, das ist das Absterben der Natur, und nach der anderen ist es das Wiederaufleben. Die zwei Punkte, wo sie ineinander übergehen, das sind Geburt und Tod.
Die Zukunft kommt uns fortwährend entgegen. Wenn das Leben bloß nach einer Richtung ginge, würde nie etwas Neues entstehen. Der Mensch hat auch Genie — das ist seine Zukunft, seine Intuitionen, die ihm entgegenströmen. Die verarbeitete Vergangenheit ist [der von der anderen Seite herkommende Strom; sie bestimmt] das Wesen [, wie es bisher geworden ist].

