The Fourth Dimension
GA 324a
22 October 1908, Berlin
Translated by Steiner Online Library
On Higher-Dimensional Space
The subject we are to discuss today will present us with a number of difficulties. Consider the lecture as an episode; it is being held at your request. If you only want to grasp the subject formally in its depth, some mathematical knowledge is necessary. But if you want to grasp it in its reality, you have to penetrate very deeply into occultism. So today we can only talk about it very superficially, only give a suggestion for this or that.
It is very difficult to talk about multidimensionality at all, because if you want to get an idea of what more than three dimensions are, you have to delve into abstract areas, and there the concepts must be very precisely and strictly defined, otherwise you end up in a bottomless pit. And that's where many friends and enemies have ended up.
The concept of multidimensional space is not as foreign to the world of mathematicians as one might think.® In mathematical circles, there is already a way of calculating with a multidimensional type of calculation. Of course, the mathematician can only speak of this space in a very limited sense; he can only discuss the possibility. Whether it really is can only be determined by someone who can see into a multidimensional space. Here we are already dealing with a lot of concepts that, if we grasp them precisely, really provide us with clarity about the concept of space.
What is space? We usually say: there is space around me, I walk around in space — and so on. If you want a clearer idea, you have to go into some abstractions. We call the space in which we move three-dimensional. It has an extension in height and depth, to the right and left, to the front and back, it has length, width and height. When we look at bodies, these bodies are extended for us in this three-dimensional space; they have a certain length, a certain width and height for us.
However, we have to deal with the details of the concept of space if we want to arrive at a more precise concept. Let us look at the simplest body, the cube. It shows us most clearly what length, width and height are. We find a base of the cube that is the same in length and width. If we move the base up, just as far as the base is wide and long, we get the cube, which is therefore a three-dimensional object. The cube is the clearest way for us to learn about the details of a three-dimensional object. We examine the boundaries of the cube. These are formed everywhere by surfaces bounded by sides of equal length. There are six such surfaces.
What is a surface? Those who are not capable of very sharp abstractions will already falter here. For example, you cannot cut the boundaries of a wax cube as a fine layer of wax. You would still get a layer of a certain thickness, so you would get a body. We will never get to the boundary of the cube this way. The real boundary has only length and width, no height. Thickness is eliminated. We thus arrive at the formulaic sentence: The area is the boundary [of a three-dimensional object] in which one dimension is eliminated.
What then is the boundary of a surface, for example of a square? Here we must again take the most extreme abstraction. [The boundary of a surface] is a line that has only one dimension, length. The width is canceled. What is the boundary of a line? It is the point, which has no dimension at all. So you always get the boundary of a thing by leaving out a dimension.
So you could say to yourself, and this is also the line of thought that many mathematicians have followed, especially Riemann,* who has achieved the most solid work here: We take the point, which has none, the line, which has one, the plane, which has two, the solid, which has three dimensions. Now mathematicians asked themselves: Could it not be that formally one could say that one could add a fourth dimension? Then the [three-dimensional] body would have to be the boundary of the four-dimensional object, just as the surface is the boundary of the body, the line is the boundary of the surface, and the point is the boundary of the line. Of course, the mathematician then goes even further to five-, six- and seven-dimensional objects and so on. We have [even arbitrary] “-dimensional objects [where ” is a positive integer].
Now, there is already some ambiguity in the matter when we say: the point has none, the line has one, the plane two, the solid three dimensions. We can now make such a solid, for example a cube, out of wax, silver, gold and so on. They are different in terms of matter. We make them the same size, then they all occupy the same space. If we now eliminate all material, only a certain part of space remains, which is the spatial image of the body. These parts of space are the same [among themselves], regardless of what material the cube was made of. These parts of space also have length, width and height. We can now imagine these cubes as infinitely extended and thus arrive at an infinitely extended three-dimensional space. The (material) body is, after all, only a part of it.
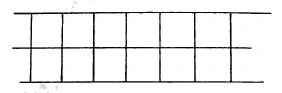
The question now is whether we can simply extend such conceptual considerations, which we make starting from space, to higher realities. In these considerations, the mathematician actually only calculates, and does so with numbers. Now the question is whether one can do that at all. I will show you how much confusion can arise when calculating with spatial quantities. Why? I only need to tell you one thing: Imagine you have a square figure here. I can make this figure, this area, wider and wider on both sides and thus arrive at an area that extends indefinitely between two lines (Figure 56).

This area is infinitely large, so it is >. Now imagine someone who hears that the area between these two lines is infinite. Of course, he thinks of infinity. If you now talk to him about infinity, he may have very wrong ideas about it. Imagine that I now add below [each square one more, so another row of] an infinite number of squares, and I get a [different] infinity that is exactly twice as large as the first (Figure 57). So we have > = 2 + 0,
In the same way I could get: “ = 3 +,
In calculating with numbers, you can just as well use infinity as finiteness. Just as it is true that space was already infinite in the first case, it is just as true that it is 2 + c, 3 - c, and so on. So we are calculating numerically here.
We see that the concept of the infinity of space [which follows from the numerical representation] does not give us any possibility of penetrating deeper [into the higher realities]. Numbers actually have no relation to space at all, they relate to it quite neutrally, like peas or any other objects. You now know that nothing changes in reality as a result of calculation. If someone has three peas, multiplication does not change that, even if the calculation is done correctly. The calculation 3 + 3 = 9 does not give nine peas. A mere consideration does not change anything here, and calculation is a mere consideration. Just as three peas are left behind, [you do not actually create nine peas,] even if you multiply correctly, three-dimensional space must also be left behind if the mathematician also calculates: two-, three-, four-, five-dimensional space. You will feel that there is something very convincing about such a mathematical consideration. But this consideration only proves that the mathematician could indeed calculate with such a multidimensional space; [but whether a multidimensional space actually exists, that is,] he cannot determine anything about the validity of such a concept [for reality]. Let us be clear about that here in all strictness.
Now we want to consider some other considerations that have been made very astutely by mathematicians, one might say. We humans think, hear, feel and so on in three-dimensional space. Let us imagine that there are beings that could only perceive in two-dimensional space, that would be organized so that they always have to remain in the plane, that they could not get out of the second dimension. Such beings are quite conceivable: they can only move [and perceive] to the right and left [and backwards and forwards] and have no idea of what is above and below.
Now it could be the same for man in his three-dimensional space. He could only be organized for the three dimensions, so that he could not perceive the fourth dimension, but for him it arises just as the third arises for the others. Now mathematicians say that it is quite possible to think of man as such a being. But now one could say that this is also only one interpretation. One could certainly say that. But here one must again proceed somewhat more precisely. The matter is not as simple as in the first case [with the numerical determination of the infinity of space]. I am intentionally only giving very simple discussions today.
This conclusion is not the same as the first purely formal [calculative] consideration. Here we come to a point where we can take hold. It is true that there can be a being that can only perceive what moves in the plane, that has no idea that there is anything above or below. Now imagine the following: Imagine that a point becomes visible to the being within the surface, which is of course perceptible because it is located in the surface. If the point only moves within the surface, it remains visible; but if it moves out of the surface, it becomes invisible. It would have disappeared for the surface being. Now let us assume that the point reappears, thus becoming visible again, only to disappear again, and so on. The being cannot follow the point [as it moves out of the surface], but the being can say to itself: the point has now gone somewhere I cannot see. The being with the surface vision could now do one of two things. Let us put ourselves in the place of the soul of this flat creature. It could say: There is a third dimension into which the object has disappeared, and then it has reappeared afterwards. Or it could also say: These are very foolish creatures who speak of a third dimension; the object has always disappeared, perished and been reborn [in every case]. One would have to say: the being sins against reason. If it does not want to assume a continuous disappearance and re-emergence, the being must say to itself: the object has submerged somewhere, disappeared, where I cannot see.
A comet, when it disappears, passes through four-dimensional space.
We see here what we have to add to the mathematical consideration. There should be something in the field of our observations that always emerges and disappears again. You don't need to be clairvoyant for that. If the surface being were clairvoyant, it wouldn't need to conclude, because it would know from experience that there is a third dimension. It is the same for humans. Unless they are clairvoyant, they would have to say: I remain in the three dimensions; but as soon as I observe something that disappears from time to time and reappears, I am justified in saying: there is a fourth dimension here.Everything that has been said so far is as unassailable as it can possibly be. And the confirmation is so simple that it will not even occur to man in his present deluded state to admit it. The answer to the question: Is there something that always disappears and reappears? — is so easy. Just imagine, a feeling of joy arises in you and then it disappears again. It is impossible that anyone who is not clairvoyant will perceive it. Now the same sensation reappears through some event. Now you, just like the surface creature, could behave in different ways. Either you say to yourself that the sensation has disappeared somewhere where I cannot follow it, or you take the view that the sensation passes away and arises again and again.
But it is true: every thought that has vanished into the unconscious is proof that something disappears and then reappears. At most, the following can be objected to: if you endeavor to object to such a thought, which is already plausible to you, with everything that could be objected to from a materialistic point of view, you are quite right. I will make the most subtle objection here, all the others are very easy to refute. For example, one says to oneself: everything is explained in a purely materialistic way. Now I will show you that something can quite well disappear within material processes, only to reappear later. Imagine that some kind of vapor piston is always acting in the same direction. It can be perceived as a progressive piston as long as the force is acting. Now suppose I set a piston that is exactly the same but acting in the opposite direction. Then the movement is canceled out and a state of rest sets in. So here the movement actually disappears.
In the same way, one could say here: For me, the sensation of joy is nothing more than molecules moving in the brain. As long as this movement takes place, I feel this joy. Now, let us assume that something else causes an opposite movement of the molecules in the brain, and the joy disappears. Wouldn't someone who doesn't go very far with their considerations find a very meaningful objection here? But let's take a look at what this objection is actually about. Just as one [piston] movement disappears when the opposite [piston movement] occurs, so the [molecular movement underlying the sensation] is extinguished by the opposite [molecular movement]. What happens when one piston movement extinguishes the other? Then both movements disappear. The second movement also disappears immediately. The second movement cannot extinguish the first without itself being extinguished. [A total standstill results, no movement whatsoever remains.] Yes, but then a [new] sensation can never extinguish the [already existing] sensation [without perishing itself]. So no sensation that is in my consciousness could ever extinguish another [without extinguishing itself in the process]. It is therefore a completely false assumption that one sensation could extinguish another [at all]. [If that were the case, no sensation would remain, and a totally sensationless state would arise.]
Now, at most, it could be said that the first sensation is pushed into the subconscious by the second. But then one admits that something exists that eludes our [immediate] observation.
We have not considered any clairvoyant observations today, but have only spoken of purely mathematical ideas. Now that we have admitted the possibility of such a four-dimensional world, we ask ourselves: Is there a way to observe something [four-dimensional] without being clairvoyant? — Yes, but we have to use a kind of projection to help us. If you have a piece of a surface, you can rotate it so that the shadow becomes a line. Similarly, you can get a point from a line as a shadow. For a [three-dimensional] body, the silhouette is a [two-dimensional] surface. Likewise, one can say: So it is quite natural, if we are aware that there is a fourth dimension, that we say: [Three-dimensional] bodies are silhouettes of four-dimensional entities.

Here we have arrived at the idea of [four-dimensional space] in a purely geometrical way. But [with the help of geometry] this is also possible in another way. Imagine a square, which has two dimensions. If you imagine the four [bounding] lines laid down next to each other [i.e., developed], you have laid out the [boundary figures] of a two-dimensional figure in one dimension (Figure 58). Let's move on. Imagine we have a line. If we proceed in the same way as with the square, we can also decompose it into two points [and thus decompose the boundaries of a one-dimensional structure into
zero dimensions]. You can also decompose a cube into six squares (Figure 59). So there we have the cube in terms of its boundaries decomposed into surfaces, so that we can say: a line is decomposed into two points, a surface into four lines, a cube into six surfaces. We have the numerical sequence two, four, six here.
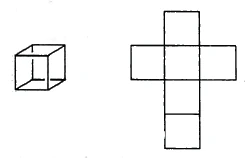
Now we take eight cubes. Just as [the above developments each consist of] unfolded boundaries, here the eight cubes form the boundary of the four-dimensional body (Figure 60). The [development of these] boundaries forms a double cross, which, we can say, indicates the boundaries of the regular [four-dimensional] body. [This body, a four-dimensional cube, is named the Hinton Tessaract after Hinton.]
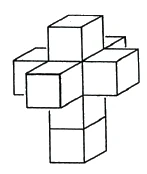
We can therefore form an idea of the boundaries of this body, the tessaract. We have here the same idea of the four-dimensional body as a two-dimensional being could have of a cube, for example by unfolding the boundaries.
Über den Mehrdimensionalen Raum
Der Gegenstand, der uns heute beschäftigen soll, wird uns mancherlei Schwierigkeiten machen. Betrachten Sie den Vortrag als eine Episode; er wird ja auf Wunsch gehalten. Wenn man den Gegenstand nur formal in seiner Tiefe erfassen will, so sind einige mathematische Vorkenntnisse nötig. Wenn man ihn aber in seiner Realität erfassen will, so muß man schon sehr tief eindringen in den Okkultismus. Wir können also heute nur sehr oberflächlich davon reden, nur eine Anregung geben für diesen oder jenen.
Es ist sehr schwierig, überhaupt über die Mehrdimensionalität zu sprechen, weil man sich, wenn man in der Vorstellung sich eine Anschauung von dem machen will, was mehr als drei Dimensionen sind, sich da in abstrakten Gebieten zu ergehen hat, und da müssen die Begriffe sehr präzise und streng gefaßt werden, sonst kommt man ins Bodenlose. Und dahin sind ja auch viele Freunde und Feinde gekommen.
Der Begriff des mehrdimensionalen Raumes ist ja der Mathematikerwelt gar nicht so fremd, als man gewöhnlich glaubt.® Es gibt in Mathematikerkreisen schon ein Rechnen mit einer mehrdimensionalen Rechnungsart. Natürlich kann der Mathematiker nur in einem sehr begrenzten Sinn von diesem Raum sprechen, er kann nur die Möglichkeit erörtern. Ob er wirklich ist, kann nur der feststellen, der in einen mehrdimensionalen Raum hineinschauen kann. Hier haben wir es schon mit lauter Begriffen zu tun, die, wenn man sie nur genau faßt, wirklich uns Klarheit verschafffen über den Raumbegriff.
Was ist der Raum? Man sagt gewöhnlich: Um mich herum ist Raum, ich gehe im Raum herum — und so weiter. Wer eine deutlichere Vorstellung haben will, der muß schon auf einige Abstraktionen eingehen. Wir nennen den Raum, in dem wir uns bewegen, dreidimensional. Er hat eine Ausdehnung nach Höhe und Tiefe, nach rechts und links, nach vorne und hinten, er hat Länge, Breite und Höhe. Wenn wir Körper betrachten, so sind diese Körper für uns in diesem dreidimensionalen Raum ausgedehnt, sie haben für uns eine gewisse Länge, eine gewisse Breite und Höhe.
Wir müssen uns aber mit den Einzelheiten des Raumbegriffes beschäftigen, wenn wir zu einem genaueren Begriff kommen wollen. Sehen wir auf den einfachsten Körper, den Würfel. Er zeigt uns am deutlichsten, was Länge, Breite und Höhe sind. Wir finden eine Grundfläche des Würfels, die in der Länge und Breite sich gleich ist. Bewegen wir die Grundfläche in die Höhe, gerade so weit, wie die Grundfläche breit und lang ist, so bekommen Sie den Würfel, der also ein dreidimensionales Gebilde ist. An dem Würfel können wir am klarsten uns unterrichten über die Einzelheiten eines dreidimensionalen Gebildes. Wir untersuchen die Grenzen des Würfels. Diese werden überall gebildet von Flächen, die von gleich langen Seiten begrenzt werden. Sechs solcher Flächen sind vorhanden.
Was ist eine Fläche? Schon hier wird der straucheln, der nicht zu ganz scharfen Abstraktionen fähig ist. Man kann zum Beispiel die Grenzen nicht von einem Wachswürfel als feine Wachsschicht abschneiden. Man bekäme dann ja immer noch eine Schicht von gewisser Dicke, erhielte also einen Körper. Auf diese Weise kommen wir nie zur Grenze des Würfels. Die wirkliche Grenze hat nur Länge und Breite, keine Höhe. Die Dicke ist gestrichen. Wir kommen also zu dem formelhaften Satze: Die Fläche ist die Grenze [eines dreidimensionalen Gebildes], bei der eine Dimension fortfällt.
Was ist nun die Grenze der Fläche, zum Beispiel des Quadrats? Hier müssen wir wieder die äußerste Abstraktion nehmen. [Die Grenze einer Fläche] ist eine Linie, die nur eine Dimension, die Länge, hat. Die Breite ist gestrichen. Was ist die Grenze der Linie? Es ist der Punkt, er hat gar keine Dimension. Man bekommt also jedesmal die Grenze eines Gebildes, indem man eine Dimension fortläßt.
Also könnte man sich sagen, und das ist auch der Gedankengang, den viele Mathematiker gegangen sind, besonders auch Riemann,*“ der hier das Gediegenste geleistet hat: Wir nehmen den Punkt, der gar keine, die Linie, die eine, die Fläche, die zwei, den Körper, der drei Dimensionen hat. Nun fragten sich die Mathematiker: Könnte es nicht so sein, daß man rein formal sagen könnte, man kann noch eine vierte Dimension hinzufügen? Dann müßte der [dreidimensionale] Körper die Grenze des vierdimensionalen Gebildes sein, wie die Fläche die Grenze des Körpers, die Linie die Grenze der Fläche und der Punkt die Grenze der Linie ist. Natürlich kommt der Mathematiker dann noch weiter zu fünf-, sechs- und siebendimensionalen Gebilden und so weiter. Wir haben [sogar beliebige] »-dimensionale Gebilde [wo » eine positive ganze Zahl ist].
Nun kommt schon eine Unklarheit in die Sache, wenn wir sagen: Der Punkt hat gar keine, die Linie hat eine, die Fläche zwei, der Körper drei Dimensionen. Wir können nun einen solchen Körper, zum Beispiel einen Würfel, aus Wachs, Silber, Gold und so weiter machen. Sie sind der Materie nach verschieden. Wir machen sie gleich groß, dann nehmen sie alle den selben Raum ein. Lassen Sie nun alle Materie fort, so bleibt nur ein bestimmter Raumteil, der das Raumbild des Körpers ist, übrig. Diese Raumteile sind [alle untereinander] gleich, aus welchem Stoff der Würfel auch bestand. Diese Raumteile haben auch Länge, Breite und Höhe. Wir können uns nun diese Würfel unendlich ausgedehnt denken und kommen so zu einem unendlich ausgedehnten dreidimensionalen Raum. Der (materielle] Körper ist ja nur ein Teil davon.
Es fragt sich nun, ob wir ohne weiteres solche begrifflichen Erwägungen, die wir, vom Raume ausgehend, machen, ausdehnen können auf höhere Wirklichkeiten. Der Mathematiker rechnet bei diesen Erwägungen eigentlich nur, und zwar mit Zahlen. Nun fragt es sich, ob man das überhaupt darf. Ich will Ihnen zeigen, eine wie große Verwirrung schon entstehen kann, wenn man mit den Raumgrößen zahlenmäßig rechnet. Warum? Ich brauche Ihnen nur eines zu sagen: Denken Sie sich, Sie haben hier eine quadratische Figur. Ich kann diese Figur, diese Fläche, nach beiden Seiten immer breiter machen und komme so zu einer Fläche, die sich unbegrenzt zwischen zwei Linien ausdehnt (Figur 56).

Diese Fläche ist doch unendlich groß, ist also >. Jetzt denken Sie sich jemand, der höre, der Flächenraum zwischen diesen beiden Linien ist unendlich [groß]. Da denkt er sich natürlich die Unendlichkeit. Sprechen Sie nun zu ihm von der Unendlichkeit, so kann er sich unter Umständen ganz falsche Vorstellungen davon bilden. Denken Sie sich, ich nehme jetzt noch unten [zu jedem Quadrat je eines dazu, also eine weitere Quadratreihe von] unendlich vielen Quadraten, so erhalte ich eine [andere] Unendlichkeit, die genau doppelt so groß ist, wie die erstere (Figur 57). Es ergibt sich also > = 2 + 0,
Auf dieselbe Weise könnte ich bekommen: » = 3 + ,
Sie können überhaupt, wenn Sie mit Zahlen rechnen, ebensogut die Unendlichkeit benutzen wie eine Endlichkeit. So wahr [es ist, daß] der Raum schon im ersten Falle unendlich war, ebenso wahr ist es, daß er nachher 2 + c, 3 - c& und so weiter ist. Wir rechnen hier also zahlenmäßig.

Wir sehen, der [sich an die zahlenmäßige Erfassung anschließende] Begriff der Unendlichkeit des Raumes gibt uns gar keine Möglichkeit, hier tiefer [in die höheren Wirklichkeiten] einzudringen. Zahlen haben eigentlich gar keine Beziehung zum Raume, verhalten sich ganz neutral zu ihm, wie Erbsen oder irgendwelche anderen Gegenstände. Sie wissen ja nun, daß sich durch Rechnen an der Realität nichts ändert. Hat jemand drei Erbsen, so kann er daran durch die Multiplikation nichts ändern, wenn er auch richtig rechnet. [Die Rechnung] 3 + 3 = 9 gibt noch‘keine neun Erbsen. Eine bloße Überlegung ändert hier nichts, und Rechnen ist eine bloße Überlegung. Ebenso wie die drei Erbsen zurückbleiben, [man in Wirklichkeit keine neun Erbsen erzeugt,] wenn auch richtig multipliziert wird, so muß der dreidimensionale Raum ebenso zurückbleiben, wenn der Mathematiker auch rechnet: zwei-, drei-, vier-, fünfdimensionaler Raum. Sie werden fühlen, daß eine solche mathematische Überlegung etwas sehr Bestechendes hat. Diese Überlegung beweist aber nur, daß der Mathematiker zwar mit einem solchen mehrdimensionalen Raum rechnen könnte; [ob es aber einen mehrdimensionalen Raum tatsächlich gibt, das heißt,] über die Gültigkeit eines solchen Begriffes [für die Wirklichkeit] kann er nichts ausmachen. Das wollen wir uns hier in aller Strenge klarmachen.
Jetzt wollen wir noch einige andere Überlegungen ins Auge fassen, die von Mathematikerseite sehr scharfsinnig, könnte man sagen, gemacht worden sind. Wir Menschen denken, hören, fühlen und so weiter im dreidimensionalen Raum. Denken wir uns einmal, daß es Wesen gäbe, die nur im zweidimensionalen Raum wahrnehmen könnten, die so organisiert wären, daß sie immer nur in der Fläche bleiben müssen, daß sie nicht aus der zweiten Dimension herauskommen könnten. Solche Wesen sind durchaus denkbar: sie können sich nur nach rechts und links [und nach hinten und vorne] bewegen [und wahrnehmen] und haben keine Ahnung davon, was oben und unten sich befindet.
Nun könnte es dem Menschen in seinem dreidimensionalen Raum auch so gehen. Er könnte nur für die drei Dimensionen organisiert sein, so daß er die vierte Dimension nur nicht wahrnehmen könnte, die aber für ihn sich ebenso hinzu ergibt, wie für die anderen die dritte sich hinzu ergibt. Nun sagen die Mathematiker, das ist durchaus denkmöglich, den Menschen als solches Wesen zu denken. Nun könnte man aber wieder sagen, das ist nun auch nur so eine Auslegung. Man könnte das gewiß sagen. Aber hier muß man doch wieder etwas genauer zu Werke gehen. So einfach wie im ersten Falle [mit der zahlenmäßigen Erfassung der Unendlichkeit des Raumes] liegt die Sache hier doch nicht. Ich gebe absichtlich heute nur ganz einfache Erörterungen.
Es ist mit dieser Schlußfolgerung nicht so, wie mit der ersten rein formalen [rechnerischen] Erwägung. Wir kommen hier zu einem Punkte, wo wir einhaken können. Es ist richtig, daß es ein Wesen geben kann, das nur wahrrniehmen kann, was in der Fläche sich bewegt, das keine Ahnung hat, daß es oben oder unten noch etwas gibt. Nun denken Sie sich einmal folgendes: Denken Sie sich, innerhalb der Fläche wird für das Wesen ein Punkt sichtbar, der natürlich wahrnehmbar ist, weil er in der Fläche sich befindet. Bewegt der Punkt sich nur in der Fläche, so bleibt er sichtbar, bewegt er sich aber aus der Fläche heraus, so wird er unsichtbar. Er wäre verschwunden für das Flächenwesen. Denken wir nun, der Punkt tauchte nachher wieder auf, werde also wieder sichtbar, verschwände dann wieder und so weiter. Verfolgen kann das Wesen den [aus der Fläche herausgehenden] Punkt nicht, aber sagen kann sich das Wesen: der Punkt ist inzwischen irgendwo gewesen, wo ich nicht hinschauen kann. Das Flächenwesen könnte nun ein zweifaches tun. Versetzen wir uns einmal in die Seele dieses Flächenwesens. Es könnte einmal sagen: Es gibt eine dritte Dimension, in die der Gegenstand untergetaucht ist, dann ist er nachher wieder aufgetaucht. - Oder es könnte auch sagen: Das sind ganz dumme Wesen, die von einer dritten Dimension sprechen, der Gegenstand ist [in jedem Falle] immer verschwunden, untergegangen und [jedesmal] wieder neu entstanden. - Man müßte dann doch sagen: Das Wesen sündigt gegen den Verstand. Wenn es also nicht ein fortwährendes Verschwinden und Neuentstehen annehmen will, muß sich das Wesen doch sagen: Der Gegenstand ist irgendwo untergetaucht, verschwunden, wo ich nicht hineinschauen kann.
Ein Komet, wenn er verschwindet, geht durch den vierdimensionalen Raum.“ Wir sehen hier, was wir zu der mathematischen Betrachtung hinzufügen müssen. Es müßte sich im Felde unserer Beobachtungen etwas finden, was immer auftaucht und wieder verschwindet. Dazu braucht man gar nicht hellsehend zu sein. Wäre das Flächenwesen hellsehend, so brauchte es ja nicht [bloß] zu schließen, es wüßte ja aus der Erfahrung, daß es eine dritte Dimension gibt. Ebenso ist es für den Menschen. Solange er nicht hellsehend ist, müßte er sich sagen: Ich bleibe in den drei Dimensionen; sobald ich aber etwas beobachte, das von Zeit zu Zeit verschwindet und wieder auftaucht, so bin ich berechtigt zu sagen: hier gibt es eine vierte Dimension.
Alles, was bisher gesagt worden ist, ist so unangreifbar wie nur irgend möglich. Und die Bestätigung ist so einfach, daß es dem Menschen in seinem heutigen verblendeten Zustande gar nicht einfallen wird, das zuzugeben. Die Antwort auf die Frage: Gibt es so etwas, was immer verschwindet und wieder auftaucht? — ist so leicht. Denken Sie einmal, es taucht eine Freude in Ihnen auf, und dann verschwindet sie wieder. Es ist unmöglich, daß irgend jemand, der nicht hellsehend ist, sie noch wahrnehmen wird. Nun taucht dieselbe Empfindung durch irgendein Ereignis wieder auf. Nun könnten Sie, genau wie das Flächenwesen, sich in verschiedener Weise verhalten. Entweder [Sie sagen sich,] die Empfindung ist verschwunden irgendwohin, wo ich sie nicht verfolgen kann, oder aber [Sie vertreten die Ansicht, daß] die Empfindung vergeht und immer wieder neu entsteht.
Es ist nun aber einmal wahr: jeder ins Unbewußte hingeschwundene Gedanke ist ein Beweis dafür, daß etwas verschwindet und [dann] wieder auftaucht. Gegen alles dies ist höchstens folgendes einzuwenden. Wenn Sie sich bemühen, gegen einen solchen Ihnen schon plausiblen Gedanken alles einzuwenden, was von einer materialistischen Anschauung eingewendet werden könnte, so tun Sie ganz recht. Ich will hier einmal den allerspitzfindigsten Einwand machen, alle anderen [Einwände] sind sehr leicht zu widerlegen. Man sagt sich zum Beispiel: alles wird auf rein materialistische Weise erklärt. Nun will ich Ihnen zeigen, daß ganz gut innerhalb der materiellen Vorgänge etwas verschwinden kann, was nachher wieder auftaucht. Stellen Sie sich einmal vor, irgendein Dampfkolben wirkt, stößt immer nach derselben Richtung hin. Er ist als fortschreitender Kolben wahrnehmbar, solange die Kraft wirkt. Nehmen wir nun an, ich setze entgegen einen ganz gleichen, [aber] entgegengesetzt wirkenden Kolben. Dann hebt sich die Bewegung auf, es tritt Stillstand ein. Hier verschwindet also tatsächlich die Bewegung.
Ganz entsprechend könnte man hier sagen: Für mich ist die Empfindung von Freude nichts anderes, als daß sich etwa im Gehirn Moleküle bewegen. Solange diese Bewegung stattfindet, empfinde ich diese Freude. Nehmen wir nun an, irgend etwas anderes bewirkt im Gehirn eine entgegengesetzte Bewegung der Moleküle, so verschwindet die Freude. Nicht wahr, es könnte jemand, der nicht sehr weit ginge mit seinen Erwägungen, hierin schon einen ganz bedeutungsvollen Einwand [gegen unsere obigen Überlegungen] finden. Aber sehen wir uns einmal an, wie es mit diesem Einwand eigentlich steht. Also genau wie eine [Kolben-] Bewegung durch die entgegengesetzte [Kolbenbewegung] verschwindet, so soll die [der] Empfindung [zugrundeliegende Molekülbewegung] durch die entgegengesetzte [Molekülbewegung] ausgelöscht werden. Was geschieht nun, wenn eine Bewegung des Kolbens die andere auslöscht? Dann verschwinden eben beide Bewegungen. Die zweite Bewegung verschwindet auch sofort. Die zweite Bewegung kann die erste gar nicht auslöschen, ohne daß sie sich [dabei] selbst auslöscht. [Es resultiert ein totaler Stillstand, keinerlei Bewegung bleibt übrig.] Ja, dann kann aber niemals eine [neue] Empfindung die [schon vorhandene] Empfindung auslöschen [ohne selbst zugrunde zu gehen]. Also könnte niemals irgendeine Empfindung, die in meinem Bewußtsein ist, eine andere auslöschen [ohne dabei sich selbst auszulöschen]. Es ist also eine ganz falsche Annahme, daß [überhaupt] eine Empfindung eine andere auslöschen könnte. [Wenn das nämlich der Fall wäre, bliebe keine Empfindung übrig, es träte ein total empfindungsloser Zustand ein.]
Jetzt könnte höchstens noch gesagt werden, daß die erste Empfindung durch die zweite ins Unterbewußtsein gedrängt wird. Aber dann gibt man eben zu, daß etwas besteht, was sich unserer [unmittelbaren] Beobachtung entzieht.
Wir haben heute gar nicht Rücksicht genommen auf irgendwelche hellseherische Beobachtungen, sondern nur von rein mathematischen Vorstellungen gesprochen. Da wir nun die Möglichkeit einer solchen vierdimensionalen Welt zugegeben haben, so fragen wir uns: Gibt es eine Möglichkeit, so etwas [Vierdimensionales] zu beobachten, ohne daß man hellsehend ist? — Ja, wir müssen dazu aber eine Art Projektion zu Hilfe nehmen. Wenn Sie ein Flächenstück haben, so können Sie es so drehen, daß das Schattenbild zur Linie wird. Ebenso können Sie von einer Linie als Schattenbild einen Punkt bekommen. Für einen [dreidimensionalen] Körper ist das Schattenbild eine [zweidimensionale] Fläche. Ebenso kann man sagen: Also ist es durchaus natürlich, wenn wir uns klar darüber sind, daß es eine vierte Dimension gibt, daß wir sagen: [Dreidimensionale] Körper sind Schattenbilder vierdimensionaler Gebilde.

Hier sind wir [nun wieder] auf rein geometrische Weise zur Vorstellung [eines vierdimensionalen Raumes] gekommen. [Mit Hilfe der Geometrie] ist dies aber auch noch auf andere Weise möglich. Denken Sie sich ein Quadrat, das ja zwei Dimensionen hat. Denken Sie sich die vier [es begrenzenden] Linien nebeneinandergelegt [, das heißt abgewickelt], so haben Sie [die Grenzgebilde] eines zweidimensionalen Gebildes in eine Dimension auseinandergelegt (Figur 58). Gehen wir weiter. Denken Sie, wir haben eine Linie. Gehen wir ebenso vor wie bei dem Quadrat, so können wir Sie auch auseinanderlegen, und zwar in zwei Punkte [und haben damit die Grenzen eines eindimensionalen Gebildes in
null Dimensionen auseinandergelegt]. Einen Würfel können Sie sich auch auseinanderlegen, und zwar in sechs Quadrate (Figur 59). Da haben.wir also den Würfel hinsichtlich seiner Grenzen in Flächen auseinandergelegt, so daß wir sagen können: Eine Linie wird in zwei Punkte, eine Fläche in vier Linien, ein Würfel in sechs Flächen auseinandergelegt. Wir haben hier die Zahlenfolge zwei, vier, sechs.

Jetzt nehmen wir acht Würfel. Genau wie [die obigen Abwicklungen jedesmal aus] auseinandergelegten Grenzen bestehen, so bilden hier die acht Würfel das Grenzgebilde des vierdimensionalen Körpers (Figur 60). Die [Abwicklung dieser] Grenzen bildet ein Doppelkreuz, das, können wir sagen, die Grenzen des regelmäßigen [vierdimensionalen] Körpers angibt. [Dieser Körper, ein vierdimensionaler Würfel, wird nach Hinton Tessarakt genannt.]

Wir können uns also eine Vorstellung bilden von den Grenzen dieses Körpers, des Tessarakts. Wir haben hier dieselbe Vorstellung von dem vierdimensionalen Körper, wie das zweidimensionale Wesen sie haben könnte von einem Würfel, zum Beispiel durch Auseinanderlegen [das heißt Abwicklung] der Grenzen.

