Second Scientific Lecture-Course:
Warmth Course
GA 321
3 March 1920, Stuttgart
Lecture III
My dear friends,
[ 1 ] Today in order to press toward the goal of the first of these lectures, we will consider some of the relations between the being of heat and the so-called state of aggregation. By this state of aggregation I mean what I referred to yesterday as called in the ancient view of the physical world, earth, water, air. You are acquainted with the fact that earth, water, and air, or as they are called today, solid, fluid, and gaseous bodies may be transformed one into another. In this process however, a peculiar phenomenon shows itself so far as heat relations are concerned. I will first describe the phenomenon and then we will demonstrate it in a simple fashion. If we select any solid body and heat it, it will become warmer and warmer and finally come to a point where it will go over from the solid to the fluid condition. By means of a thermometer we can determine that as the body absorbs heat, its temperature rises. At the moment when the body begins to melt, to become fluid, the thermometer ceases rising. It remains stationary until the entire body has become fluid, and only begins to rise again when all of the solid is melted. Thus we can say: during the process of melting, the thermometer shows no increase in temperature. It must not be concluded from this however, that no heat is being absorbed. For if we discontinue heating, the process of melting will stop. (I will speak more of this subsequently.) Heat must be added in order to bring about melting, but the heat does not show itself in the form of an increase in temperature on the thermometer. The instrument begins to show an increase in temperature only when the melting has entirely finished, and the liquid formed from the solid begins to take up the heat. Let us consider this phenomenon carefully. For you see, this phenomenon shows discontinuity to exist in the process of temperature rise. We will collect a number of such facts and these can lead us to a comprehensive view of heat unless we go over to some reasoned-out theory. We have prepared here this solid body, sodium thiosulphate, which solid we will melt. You see here a temperature of about 25° C. Now we will proceed to heat this body and I will request someone to come up and watch the temperature to verify the fact that while the body is melting the temperature does not rise.(Note: The thermometer went to 48° C. which is the melting point of sodium thiosulphate, and remained there until the substance had melted.) Now the thermometer rises rapidly, since the melting is complete, although it remained stationary during the entire process of melting.
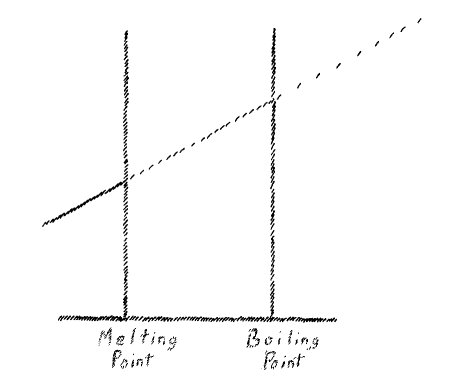
[ 2 ] Suppose we illustrate this occurrence in a simple way, as follows: The temperature rise we will consider as a line sloping upward in this fashion (Fig. 1). Assume we have raised the temperature to the melting point as it is called. So far as the thermometer shows, the temperature again rises. It can be shown that through this further temperature rise, with its corresponding addition of heat, the liquid in question expands. Now if we heat such a melted body further, the temperature rises again from the point at which melting took place (dotted line.) It rises as long as the body remains fluid. We can then come upon another point at which the liquid begins to boil. Again we have the same phenomenon as before. The thermometer shows no further temperature rise until the entire liquid is vaporized. At the moment when the fluid has vaporized, we would find by holding the thermometer in the vapor that it again shows a temperature rise (dot-dash line.) You can see here that during vaporizing the instrument does not rise. There I find a second place where the thermometer remains stationary. (Note: the thermometer remained at 100° C. in a vessel of boiling water.)
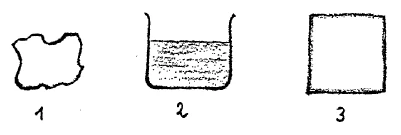
[ 3 ] Now I will ask you to add to the fact I have brought before you, another which you will know well from ordinary experience. If you consider solids, which form our starting point, you know that they hold their shape of themselves, whatever form is given them they maintain. [ 4 ] If I place a solid here before you it remains as it is. If you select a fluid, that is, a body that has by the application of heat been made to go through the melting point, you know that I cannot handle it piece by piece, but it is necessary to place it in a vessel, and it takes the form of the vessel, forming a horizontal upper surface. (Fig. 3) If I select a gas—a body that has been vaporized by passing through the boiling point, I cannot keep it in an open vessel such as I use for the liquid, it will be lost. Such a gas or vapor I can hold only in a vessel closed in on all sides, otherwise the gas spreads out in all directions. (Fig. 4) This holds, at least for superficial observation, and we will consider the matter first in this way. And now I would ask you to make the following consideration of these things with me. We make this consideration in order to bring facts together so that we can reach a general conception of the nature of heat. Now have we determined the rise in temperature? We have determined it by means of the expansion of quicksilver. The expansion has taken place in space. And since at our ordinary temperature quicksilver is a liquid, we must keep clear in our minds that it is confined in a vessel, and the three dimensional expansion is summed up so that we get an expansion in that direction. By reducing the expansion of quicksilver in three dimensions to a single dimension, we have made this expansion measure the temperature rise.
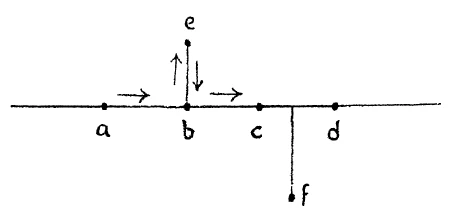
[ 5 ] Let us proceed from this observation which we have laid out as a fundamental and consider the following: Assume a line (Fig. 5) Naturally, a line can only exist in thought. And suppose on this line there lie a number of points \(a\), \(b\), \(c\), \(d\), etc. If you wish to reach these points you can remain in the line. If, for instance, you are at this point \(a\) you can reach c by passing along the line. You can pass back again and again reach the point a. In brief, if I desire to reach the points \(a\), \(b\), \(c\), \(d\), I can do so and remain entirely in the line. The matter is otherwise when we consider the point \(e\) or the point \(f\). You cannot remain in the line if you wish to reach point \(e\) or \(f\). You must go outside to reach these points. You have to move along the line and then out of it to get to these points.
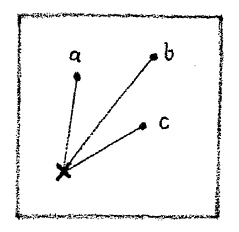
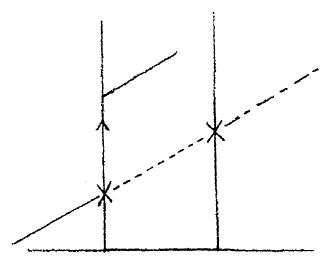
[ 6 ] Now assume you have a surface, let us say the surface of the blackboard, and again I locate on the surface of this board a number of points; \(a\), \(b\), \(c\), \(d\). (Fig. 6) In order to reach these points you may remain always in the surface of the blackboard. If you are at this point \(x\) you may trace your way to each of these points over a path that does not leave the blackboard. You cannot, however, if you wish to remain in the surface of the board, reach this point which is at a distance in front of the board. In this case you must leave the surface. This consideration leads to a view of the dimensionality of space from which one can say: To reach points in one dimension, movement in this single direction suffices, for those in two dimensions movement in two dimensions gives access to them. It is however, not possible to reach points outside a single dimension without leaving this dimension and likewise one cannot pass through points in three dimensions by moving about in a single plane. What is involved when I consider the points e and f in relation to the single dimension represented by points \(a\), \(b\), \(c\) and \(d\) ? Imagine a being who was able to observe only one dimension and who had no idea of a second or third dimension. Such a being would move in his one dimension just as you do in three dimensional space. If such a being carried the point \(a\) to the position \(b\) and the point then slipped off to e, at that moment the content of the point would simply vanish from the single dimension of the being. It would no longer exist for this being from the moment it left the single dimension of which he is aware. Likewise the points outside a surface would not exist for a being aware only of two dimensions. When a point dropped out of the plane, such a being would have no way of following it; the point would disappear form his space realm. What kind of a geometry would a unidimensional being have? He would have a one-dimensional geometry. He would be able to speak only of distance and the like, of the laws relating to such things as they applied in a single dimension. A two-dimensional being would be able to speak of the laws of plane figures and would have a two-dimensional geometry. We men have at the outset a three-dimensional geometry. A being with a unidimensional geometry would have no possibility of understanding what a point does when it leaves the single dimension. A being with a two-dimensional geometry would be unable to follow the motion of a point that left a surface and moved out in front of it as we supposed was the case when the point left a surface and moved out in front of it as we supposed was the case when the point left the surface of the blackboard. We men—I state again—have a three-dimensional geometry. Now I may just as well do what I am obliged to do on account of the reducing of the three-dimensional expansion of the quicksilver to a single dimension. I may draw two lines in two directions so as to form a system of axes, thus giving as in Fig. 7 an axis of abscissae and an axis of ordinates. At right angles to the plane of these two, suppose we have a third line which we will call a space line.1Referring again to the temperature rise diagram – tr. Just as soon as I come either to the melting point or the boiling point, at that moment I am not in a position to proceed with the line (Fig. 8).
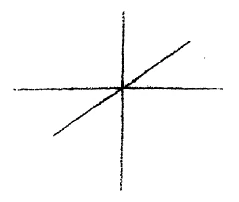
[ 7 ] Theoretically or hypothetically there is no possibility of continuing the line. Let us assume that we can say, the rise of temperature is represented by this line. We can proceed along it and still have a point of connection with our ordinary world. But we do not as a matter of fact have such a point of connection. For when I draw this temperature curve and come to the melting or boiling point, I can only continue the curve from the same point (\(x\), \(x\) in Fig. 8). I had reached when the body had begun to melt or vaporize. You can see from this, that in regard to the melting or boiling point, I am in a position not different from that of the one-dimensional being when a point moves out of his first dimension into the second dimension, or of the two-dimensional being when a point disappears for him into the third dimension. When the point comes back again and starts from the same place, or as in Fig. 5 when the point moves out to one side and returns, then it is necessary to continue the line on in its one dimension. Considered simply as an observed phenomenon, when the temperature rise disappears at the melting and boiling point, it is as though my temperatures curve were broken, and I had to proceed after a time from the same point. But what is happening to the heat during this interruption falls outside the realm in which I draw my curve. Formally speaking, I may say that I can draw this on the space line. There is, at first considered—note I say at first—an analogy present between the disappearance of the point a from the first and into the second dimension and what happens to the temperature as shown by the thermometer when the instrument stands still at the melting point and the boiling point.
[ 8 ] Now we have to bring another phenomenon in connection with this. Please note that in this linking together of phenomena we make progress, not in elaborating some kind of theory, but in bringing together phenomena so that they naturally illuminate each other. This is the distinction between the physics of Goethe that simply places phenomena side by side so that they throw light on each other, and modern physics which tends to go over into theories, and to add thought-out elaborations to the facts. For atoms and molecules are nothing else but fancies added to the facts.
[ 9 ] Let us now consider another phenomenon along with this disappearance of the temperature recorded by the thermometer during the process of melting. This other phenomenon meets us when we look at yesterday's formula. This formula was written:
$$V=V_o(1 + 3 \alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3)$$
[ 10 ] You remember that I said yesterday you should pay especial attention to the last two terms. It is especially important for us at this time to consider \(t^3\), the third power of the temperature. Imagine for a moment ordinary space. In this ordinary space you speak in mathematical terms of length, breadth, and thickness. These are actually the three dimensions of space. Now when we warm a rod, as we did yesterday, we can observe the expansion of this rod. We can also note the temperature of this rod. There is one thing we cannot bring about. We cannot bring it about that the rod while it is expanding, does not give off heat to its surroundings, that it does not stream out or radiate heat. This we cannot prevent. It is impossible for us to think—note the word—of a propagation of heat in one dimension. We can indeed think of a space extension in one dimension as one does in geometry in the case of a line. But we cannot under any circumstances imagine heat propagated along a line. When we consider this matter we cannot say that the propagation of heat is to be thought of as represented in space in reality by the line that I have drawn here. (Fig. 1) This curve does not express for me the whole process involved in the heat. Something else is active besides what I can deduce from the curve. And the activity of this something changes the entire nature and being of what is shown by this curve, which I am using as a symbol which may be considered equally well as a purely arithmetical or geometrical fact.
[ 11 ] We have, thus, a peculiar situation. When we try to grasp the heat condition, in so far as the temperature shows this condition, by means of an ordinary geometrical line, we find it cannot be done. Now this has another bearing. Imagine for a moment that I have a line. This line has a certain length: \(l\) (Fig. 9) I square this line, and then I can represent this \(l^2\) by a square surface.
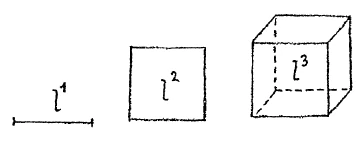
[ 12 ] Assume that I obtain \(l^3\) then I can represent the third power by a cube, a solid body. But suppose I obtain the fourth power, \(l^4\). How can I represent that? I can pass over from the line to the surface, from the surface to the solid, but what can I do by following this same method if I wish to represent the fourth power? I cannot do anything if I remain in our three-dimensional space. The mathematical consideration shows this. But we have seen that the heat condition in so far as it is revealed by temperature is not expressible in space terms. There is something else in it. If there were not, we could conceive of the heat condition passing along a rod as confined entirely to the rod. This, however, is impossible. The consequence of this is that when I really wish to work in this realm, I ought not to look upon the powers of \(t\) in the same manner as the powers of a quantity measured in space. I cannot think about the powers of \(t\) in the same way as those of \(l\) or of any other mere space quantity. When, for instance, and I will consider this tomorrow hypothetically, when I have the first power and find it not expressible as a line, then the second power \(t^2\) cannot be expressed as a surface and certainly the third power \(t^3\) cannot be expressed as a solid. In purely mathematical space, it is only after I have obtained the third power that I get outside of ordinary space, but in this other case I am quite outside of ordinary space in the case of the second power and the third as well.
[ 13 ] Therefore, you must realize that you have to conceive of \(t\) as different entirely in its nature from space quantities. You must consider \(t\) as something already squared, as a second power and the squared \(t\) you must think of as of the third power, the cubed \(t\) as of the fourth power. This takes us out of ordinary space. Consider now how this gives our formula a very special aspect. For the last member, which is in this super-space, forces me to go out of ordinary space. In such a case when I confine myself to reckoning I must go beyond three dimensional space for the last member of the formula. There is such a possibility in purely mathematical formulae.
When you observe a triangle and determine that it has three angles, you are dealing, at the start, with a conceived triangle. Since merely thinking about it is not enough to satisfy your senses, you draw it, but the drawing adds nothing to your idea. You have given, the sum of the angles is 180, or a right-angled triangle—the square of the hypotenuse equals the sum of the squares of the other two sides. These things are handled as I now handle the power of \(t\).
Let us now go back and see what we have established as fact. This is the way it is done in geometry. It is always true that when I observe an actual triangle in bridge construction or elsewhere, the abstract idea verifies itself. What I have thought of in the abstract \(t\) has at first a similarity with melting and vaporizing. (We will gradually get nearer to the essence of the reality.) Melting and vaporizing I could not express in terms of the three dimensions of space. The only way I could force them into the curve was to stop and then continue again. In order to prove the hypothesis that I made for you, it was necessary, in the case of the third power, the cube of the temperature, to go outside of three-dimensional space.
[ 14 ] You see, I am showing you how we must, as it were, break a path if we wish to place together those phenomena which simply by being put side by side illustrate the being of heat and enable us to attain to an understanding similar to that reached in the preceding course of lectures on light.
The physicist Crookes approached this subject from entirely different hypotheses. It is significant that his considerations led him to a result similar to the one we have arrived at tentatively and whose validity we will establish in the next lectures. He also concluded the temperature changes had essentially to do with a kind of fourth dimension in space. It is important at this time to give attention to these things because the relativists, with Einstein at their head, feel obliged when they go outside of three-dimensional space, to consider time as the fourth dimension. Thus, in the Einstein formulae, everywhere one finds time as the fourth dimension. Crookes, on the other hand, considered the gain or loss of heat as the fourth dimension. So much for this side-light on historical development.
[ 15 ] To these phenomena I would ask you now to add what I have formerly emphasized. I have said: An ordinary solid may be handled and it will keep its form, (Fig. 2). That is, it has a determinate boundary. A fluid must be poured into a vessel, (Fig. 3). It always forms a flat upper surface and for the rest takes the shape of the vessel. This is not so for a gas or vaporous body which extends itself in every direction. In order to hold it, I must put it into a vessel closed on all sides, (Fig. 4). [ 16 ] This completely closed vessel gives it its form. Thus, in the case of a gas, I have a form only when I shut it in a vessel closed on all sides. The solid body possesses a form simply by virtue of the fact that it is a solid body. It has a form of itself, as it were. Considering the fluid as an intermediate condition, we will note that the solid and gaseous bodies may be described as opposites. The solid body provides for itself that which I must add to the gaseous body, namely the completely surrounding boundary.
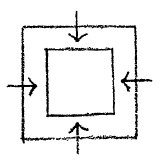
Now, however, a peculiar thing occurs in the case of a gas. When you put a gas into a smaller volume (Fig. 10), using the same amount of gas but contracting the walls all around, you must use pressure. You have to exert pressure. [ 17 ] This means nothing else but that you have to overcome the pressure of the gas. You do it by exerting pressure on the walls which give form to the gas. We may state the matter thus: that a gas which has the tendency to spread out in all directions is held together by the resistance of the bounding walls. This resistance is there of itself in the case of the solid body. So that, without any theorizing, but simply keeping in mind the quite obvious facts, I can define a polaric contrast between a gas and a solid body in the following way: That which I must add to the gas from the outside is present of itself in the solid. But now, if you cool the gas, you can pass back again to the boiling point and get a liquid from the vapor, and if you cool further to the melting point, you can get the solid from the liquid. That is to say, you are able by processes connected with the heat state to bring about a condition such that you no longer have to build the form from the outside, but the creation of form takes place of itself from within. Since I have done nothing but bring about a change in the heat condition, it is self-evident that form is related in some way to changes in the heat state. In a solid, something is present which is not present in a gas. If we hold a wall up against a solid, the solid does not of itself exert pressure against the wall unless we ourselves bring this about. When, however, we enclose a gas in a vessel, the gas presses against the solid wall. You see, we come upon the concept of pressure and have to bring this creation of pressure into relation with the heat condition. We have to say to ourselves: it is necessary to find the exact relation between the form of solid bodies, the diffusing tendency of gases and the opposition of the boundary walls that oppose this diffusion. When we know this relation we can hope really to press forward into the relation between heat and corporeality.
Dritter Vortrag
[ 1 ] Wir werden heute, um auf das Ziel zuzusteuern, dem wir in den ersten Tagen unserer Betrachtungen schon nahekommen müssen, noch einige Erscheinungen uns ansehen, welche die Beziehung des Wärmewesens zum sogenannten Aggregatzustand betreffen, also zu dem, was, wie ich Ihnen gestern gesagt habe, in der alten physikalischen Weltanschauung bezeichnet wurde als Erde, Wasser, Luft. Sie wissen ja, daß Erde, Wasser, Luft oder, wie wir es heute nennen, feste, flüssige und gasförmige Körper, in andere überzuführen sind. Dabei zeigt sich aber mit Bezug auf das Wärmewesen eine ganz besondere Erscheinung. Ich will die Erscheinung zunächst beschreiben, und wir wollen sie dann einfach konstatieren: Nehmen wir irgendeinen festen Körper und erwärmen wir ihn, so wird er eben immer wärmer und wärmer, bis er zu einem Punkte kommt, an dem er übergeht aus dem festen in den flüssigen Zustand. Wir können nun, wenn wir ein Thermometer zu Hilfe nehmen, konstatieren, wie, während der Körper immer wärmer und wärmer wird, das Thermometer steigt. In dem Augenblick, in dem der Körper beginnt flüssig zu werden, also zu schmelzen, hört das Thermometer auf zu steigen. Es wartet, bis der ganze Körper flüssig geworden ist, und es steigt erst wieder innerhalb der Flüssigkeit, die aus dem Körper geworden ist. So daß wir sagen können: Während des Vorganges des Schmelzens zeigt sich an dem Thermometer kein Ansteigen der Temperatur. Dabei darf man aber nicht glauben, daß das Wärmewesen selber unbeteiligt ist. Wenn wir nun keine Wärme zuführen würden, so würde das Schmelzen aufhören. Wir müssen also Wärme zuführen, um das Schmelzen bewirken zu können, aber diese Wärme zeigt sich nicht am "Thermometer, sondern es fängt erst an, daß sich wiederum Wärme am Thermometer zeigt, wenn das Schmelzen vollzogen ist und nun weiter erwärmt wird die Flüssigkeit, die aus dem festen Körper entstanden ist. Diese Erscheinungen müssen zunächst einmal genau ins Auge gefaßt werden. Denn Sie sehen, daß durch diese Erscheinungen in dem Fortgang des Aufsteigens der Temperatur eine Unterbrechung eintritt. Wir wollen eine Anzahl solcher Erscheinungen zusammenstellen, die uns dann, ohne daß wir übergehen zu irgendwelchen ausgedachten Theorien, zu einer Anschauung über das Wärmewesen werden führen können. Wir haben hier vorbereitet zunächst diesen festen Körper, Natriumthiosulfat. Wir werden diesen Körper zum Schmelzen bringen. Sie sehen hier eine Temperatur von etwa 25°. Nun handelt es sich darum, daß wir diesem Körper Wärme zuführen, und ich bitte irgend jemand, als Delegierten sich hierher zu begeben, um zu sehen, wie während des Schmelzens dieses Körpers die Temperatur tatsächlich nicht steigt. (Inzwischen ist das Thermometer auf 48°, den Schmelzpunkt des Natriumthiosulfats, gestiegen und dieses ist geschmolzen.) Jetzt steigt das Thermometer rasch, weil das Schmelzen vollzogen ist, während es früher stehenblieb während des ganzen Schmelzvorganges.
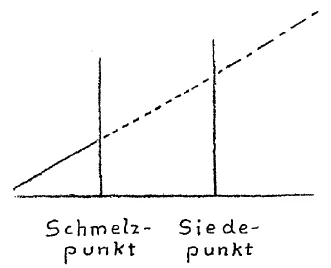
[ 2 ] Nun wollen wir einmal diesen Vorgang uns einfach versinnlichen. Wir können das auf folgende Weise tun. Das Ansteigen der Temperatur wollen wir auffassen als eine Linie, die in dieser Weise ansteigt. Nehmen wir an, wir seien mit der ansteigenden Temperatur bis zum sogenannten Schmelzpunkt gekommen. Hier beginnt der Körper zu schmelzen. Die Temperatur bleibt, soweit sie durch das Thermometer gezeigt wird, stehen. Wenn ich jetzt weiter erhitze, steigt die Temperatur wieder an. Man würde sehen, daß sich durch das Ansteigen der Temperatur, das heißt durch das Zuführen weiterer Wärme, die betreffende Flüssigkeit ausdehnt. Nun handelt es sich darum, daß wir einen solchen flüssig gewordenen Körper weiter erhitzen. Dann steigt die Temperatur wiederum und zwar ‘von demselben Punkte aus, an dem sie beim Schmelzen war (punktierte Linie). Sie steigt, so lange der Körper nun flüssig bleibt. Wir können zu einem zweiten Punkt kommen, in dem die Flüssigkeit beginnt zu sieden, zu verdampfen. Wir haben wieder dieselbe Erscheinung: Das Thermometer hört auf, eineErhöhung der "Temperatur anzuzeigen. So lange, bis die Flüssigkeit verdampft ist. In dem Augenblick, wo die Flüssigkeit verdampft ist, würden wir, wenn wir das Thermometer in den Dampf hineinhalten könnten, wiederum sehen, wie das Thermometer ansteigt (strichpunktierte Linie). Sie könnten hier wiederum beobachten, daß während des Verdampfens das Thermometer nicht ansteigt. Ich habe also hier eine zweite Grenze, an der die Thermometererhöhung stehenbleibt.
[ 3 ] Nun, zu dieser Erscheinung, die ich Ihnen eben vorgeführt habe, bitte ich Sie, eine andere hinzuzunehmen, die Ihnen aus dem gewöhnlichen Leben sehr gut bekannt sein kann: Wenn wir den festen Körper nehmen, der unseren Ausgangspunkt bildete, so ist dieser, wie Sie wissen, so, daß er seine Form, die er einmal hat, durch sich selbst beibehält (1).

[ 4 ] Wenn ich irgendeinen festen Körper hierher lege, so bleibt er, wie er ist. Wenn Sie eine Flüssigkeit nehmen, also dasjenige, was durch den Schmelzpunkt hindurchgegangen ist bei der Erwärmung, so wissen Sie, daß ich eine Flüssigkeit nicht hinlegen kann stück weise, sondern ich habe nötig, sie in einem Gefäß zu halten, und sie bleibt in der Form des Gefäßes und bildet oben eine horizontale Niveaufläche (2). Wenn ich ein Gas nehme, Dampf, der durchgegangen ist durch den Siedepunkt, so kann ich den nicht behalten in einem solchen Gefäß. Da geht er mir fort. Einen solchen Dampf kann ich nur aufbehalten in einem Gefäß, das allseitig geschlossen ist, sonst geht mir der Dampf nach allen Seiten hin fort (3). Das gilt wenigstens zunächst für den oberflächlichen Anblick, und wir wollen von diesem oberflächlichen Anblick zunächst einmal ausgehen. Und jetzt bitte ich Sie, folgende Erwägungen mit mir zu machen. Diese Erwägungen stellen wir an, um durch ihr Zusammenbringen zuletzt uns wirklich zu einer Art Erfassung des Wärmewesens hinbegeben zu können. Wodurch habe ich denn überhaupt die ansteigende 'Temperatur konstatiert? Ich habe sie konstatiert durch die Ausdehnung des Quecksilbers. Diese Ausdehnung des Quecksilbers hat sich vollzogen im Raum. Und wenn auch das Quecksilber bei unserer mittleren Temperatur eine Flüssigkeit ist, so müssen wir uns doch klar sein, daß, wenn es auch zusammengehalten wird in dem Gefäß, sich doch die Ausdehnungen nach den drei Dimensionen summieren, und wir bekommen sie als Ausdehnung nur nach der einen Seite heraus. Wir haben doch bei der Ausdehnung des Quecksilbers nach den drei Dimensionen diese nur reduziert auf die eine Dimension hin, so daß wir also das Ansteigen der Temperatur konstatieren durch die Ausdehnung eines Körpers.

[ 5 ] Gehen wir von dieser Betrachtung aus, die wir zugrunde gelegt haben, und sehen wir uns das Folgende an: Nehmen wir einmal eine Linie (siehe Zeichnung) — man kann eine Linie natürlich nur denken und sagen Sie sich, auf dieser Linie lägen eine Anzahl Punkte, \(a\), \(b\), \(c\), \(d\) und so weiter. Wenn Sie zu diesen Punkten kommen wollen, so können Sie durchaus in dieser Linie bleiben. Wenn Sie zum Beispiel hier stehen \((a)\), können Sie zu dem Punkt \(c\) gelangen, indem Sie die Linie durchlaufen. Sie können zurücklaufen und wiederum den Punkt \(a\) erreichen. Kurz, wenn ich die Punkte \(a\), \(b\), \(c\), \(d\) erreichen will, kann ich durchaus in der Linie bleiben. Anders liegt das, wenn wir den Punkt \(e\) oder den Punkt \(f\) ins Auge fassen. Sie können nicht bei der Linie verbleiben, wenn Sie zu dem Punkt \(e\) und zu dem Punkt \(f\) gelangen wollen. Sie müssen aus der Linie herausgehen, um zu dem Punkt \(e\) und zu dem Punkt \(f\) zu gelangen. Sie müssen also irgendwie auf der Linie laufen und dann aus der Linie heraustreten, um zu diesen Punkten zu gelangen.

[ 6 ] Jetzt nehmen Sie an, Sie betrachten eine Fläche, sagen wir die Fläche der Tafel, und ich registriere wiederum auf der Fläche der Tafel eine Anzahl Punkte: \(a\), \(b\), \(c\). Um diese Punkte zu erreichen, können Sie durchaus in der Fläche der Tafel bleiben. Wenn Sie hier sind \((\times)\), können Sie den Weg machen, der gar nicht aus der Tafel herausgeht, zu jedem dieser Punkte. Sie können aber nicht, wenn Sie in der Tafel verbleiben wollen, zu dieser Spitze, die hier ist (vor der Tafel) und die einen weiteren Punkt darstellt, gelangen. Da müssen Sie aus der Tafel herausgehen. Auf diese Weise ist es möglich, sich eine Anschauung über die Dimensionalität des Raumes zu machen, indem man sich sagt: Für Punkte, die in der ersten Dimension liegen, ist es möglich, durch diese eine Dimension auch zu ihnen zu gelangen. Für Punkte aber, die außerhalb der einen Dimension liegen, kann man nicht, ohne aus dieser Dimension zu gehen, zu diesen Punkten gelangen. Ebenso kann man nicht zu Punkten, die in der dritten Dimension liegen, durch ein Durchlaufen der Fläche gelangen. Was tritt ein, wenn ich nur von den Punkten \(e\) und \(f\) mit Bezug auf die eine Dimension rede, in der die Punkte \(a\), \(b\), \(c\), \(d\) liegen? Denken Sie sich einmal ein Wesen, welches in der Lage wäre, nur eine einzige Dimension zu beobachten, welches keine Vorstellung hätte von einer zweiten und dritten Dimension. Ein solches Wesen würde, geradeso wie Sie im dreidimensionalen Raume sich bewegen, sich nur in der einen Dimension bewegen. In dem Augenblick, wo dieses Wesen den Punkt a mitnimmt (siehe Zeichnung) bis hierher \((b)\) und der Punkt dann abweicht und nach \(e\) geht, in dem Augenblick würde der Inhalt dieses Punktes für dieses Wesen einfach verschwinden. Er ist nicht da für ein solches Wesen, das nur wahrnehmen könnte in einer solchen Dimension, in dem Augenblick, wo er aus dieser einen Dimension herausgeht. Ebenso sind alle Punkte, die außerhalb der beiden Dimensionen der Fläche liegen, nicht da für ein Wesen, das nur in den zwei Dimensionen der Fläche wahrnehmen kann. Und wenn ein Punkt, der in der Fläche liegt, sich einfallen läßt, aus der Fläche herauszugehen, so würde dieses Wesen kein Mittel haben, um diesen Punkt weiter zu verfolgen. Er würde aus dem Bereich seines Raumes verschwinden. Ein solches Wesen, ein Wesen, das nur wahrnehmen könnte in einer einzigen Dimension, was würde es denn für eine Geometrie haben? Es würde nur eine eindimensionale Geometrie haben. Es würde nur innerhalb der einen Dimension von Entfernungen und dergleichen und ihren Gesetzen reden können. Ein Wesen, das nur in zwei Dimensionen wahrnehmen kann, würde nur von den Gesetzen der ebenen Figuren sprechen können, würde nur eine zweidimensionale Geometrie haben. Wir Menschen haben eine dreidimensionale Geometrie zunächst. Ein Wesen mit einer eindimensionalen Geometrie hätte gar keine Möglichkeit, irgendwie dasjenige geometrisch zu versinnlichen, was ein Punkt tut, der aus der einen Dimension hinausgeht. Ein Wesen mit einer zweidimensionalen Geometrie hätte keine Möglichkeit, das zu verfolgen, was ein Punkt tut, der aus den zwei Dimensionen herausgeht und nachher da ist (vor der Tafel). Wir Menschen - ich sage es noch einmal — haben eine dreidimensionale Geometrie. Nun könnte ich ebensogut, weil ich es ja eigentlich zu tun habe, wie schon früher gesagt, bei der Ausdehnung des Quecksilbers mit drei Dimensionen, die nur auf eine Dimension reduziert sind, könnte ich, wie ich hier, nur durch die Tafel veranlaßt, auf zwei Dimensionen eine Linie gezogen habe, sie auch so ziehen, daß ich sie auf ein Raumkoordinatensystem bezöge. Ich hätte hier eine Abszissenachse, eine Ordinatenachse und senkrecht darauf eine dritte Achse, und ich würde diese Linie als eine Raumlinie ziehen können. In dem Augenblick, in dem ich ankomme entweder bei dem Schmelzpunkt oder Siedepunkt, bin ich nicht in der Lage, irgendwie mit dem Ziehen dieser Linie fortzufahren.

[ 7 ] Es gäbe, theoretisch, hypothetisch ausgedrückt eine Möglichkeit, fortzufahren. Nehmen wir einmal an, ich könnte die Sache so machen: Sagen wir, das Ansteigen der Temperatur würde durch diese Linie dargestellt (siehe Zeichnung). Ich müßte dann, indem irgendwelche Faktoren gleichbleiben, anderes hier verändern und könnte dann von einem anderen Punkt oben fortfahren. So würde ich noch einen Anhaltspunkt haben, in meiner Welt zu bleiben. Aber einen solchen Anhaltspunkt habe ich nicht. Denn ich muß einfach, wenn ich diese Temperaturkurve zeichne, von demselben Punkte ausgehen, auf dem die Temperatur steht, nachdem der betreffende Körper geschmolzen oder verdampft ist ( \(x\) \(x\) in der Zeichnung), von demselben Punkt, auf dem sie angekommen ist, wenn das Schmelzen oder Verdampfen begonnen hat. Sie sehen daraus, daß ich hier mit Schmelzpunkt und Siedepunkt einfach zu etwas genötigt bin, das sich mit nichts vergleichen läßt als mit der Lage, in der ein eindimensionales Wesen ist, wenn ihm ein Punkt aus seiner einen Dimension heraus in die zweite Dimension hinein verschwindet, oder ein zweidimensionales Wesen, wenn ihm ein Punkt in die dritte Dimension verschwindet. Wenn der Punkt wiederum hereinkommt und von derselben Stelle aus weitergeht, wenn also der Punkt \(a\) hierher verschleppt ist (siehe Zeichnung), hinausgeht, und nun gewartet wird und der Punkt wiederum zurückkommt, so muß ich von derselben Stelle seinen Lauf weiterverfolgen in der einen Dimension drinnen. Rein erscheinungsgemäß gesprochen, liegt mir ja nichts anderes vor, wenn mir die Erwärmung verschwindet beim Schmelzpunkt und Siedepunkt, als daß meine Temperaturkurve unterbrochen wird und ich sie von demselben Punkte aus nach einiger Zeit fortsetzen muß. Aber dasjenige, was während der Unterbrechung mit der Wärme geschieht, das fällt ebenso aus dem Bereich heraus, in dem ich meine Kurve ziehe — und ich sage ausdrücklich, ich kann sie als Raumkurve ziehen. Es ist zunächst - ich sage zunächst — Analogie vorhanden zwischen diesem Verschwinden des Punktes a aus der ersten in die zweite Dimension hinein und dem, was da geschieht mit der durch das "Thermometer angezeigten Wärme, während das Thermometer stillsteht beim Schmelzpunkt und Siedepunkt.

[ 8 ] Nun handelt es sich darum, mit dieser Erscheinung eine andere in Zusammenhang zu bringen. Sehen Sie, auf dieses In-ZusammenhangBringen der Erscheinungen kommt nämlich alles an; nicht auf das Ausdenken irgendwelcher Theorien, sondern auf das Zusammenbringen der Erscheinungen, so daß sie sich gegenseitig beleuchten und erklären. Das ist der Unterschied der Goetheschen Physik von der heute herrschenden, daß die Goethesche Physik die Erscheinungen einfach zusammenstellt, damit sie sich gegenseitig beleuchten, während die heutige Physik, wenn sie überhaupt wagt, zu Theorien überzugehen, darauf aus ist, zu den Erscheinungen hinzu zu theoretisieren, hinzu zu phantasieren. Denn Atome und Moleküle sind ja im wesentlichen nichts anderes, als zu den Erscheinungen hinzuerfunden, hinzuphantasiert.
[ 9 ] So wollen wir denn eine andere Erscheinung zusammenhalten mit dem Verschwinden der durch das Thermometer konstatierbaren Erwärmung während des Schmelzens. Diese andere Erscheinung tritt uns entgegen, wenn wir unsere gestrige Formel ins Auge fassen:
$$V=V_o(1 + 3 \alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3)$$
[ 10 ] Von dieser Formel sagte ich gestern, daß Sie insbesondere die zwei letzten Glieder ins Auge fassen sollen. Es ist besonders wichtig für uns heute, das \(t^3\) einmal ins Auge zu fassen, die dritte Potenz der Temperatur. Nehmen Sie einmal eine gewöhnliche Raumdimensionalität. Bei dieser gewöhnlichen Raumdimensionalität sprechen Sie, wenn es ein mathematischer Körper ist, von Länge, Breite und Höhe. Das sind ja im wesentlichen die drei Raumdimensionen. Nun können wir, wenn wir einen Stab erwärmen, wie wir das gestern getan haben, die Ausdehnung dieses Stabes betrachten. Wir können auch die Temperatur dieses Stabes betrachten. Aber wir können eines nicht herbeiführen: daß der Stab, während er sich ausdehnt, nicht Wärme in seine Umgebung abgibt, daß er nicht Wärme ausströmt, ausstrahlt. Das können wir nicht verhindern. Wir können unmöglich eine Wärmeausdehnung uns denken - bitte auf das Wort zu achten — nur nach einer Dimension. Wir können wohl eine reine Raumausdehnung - das tut man ja immer in der Geometrie — nach einer Dimension, nämlich als Linie denken, wir können aber niemals einen Wärmezustand auch nur denken, der sich bloß längs einer Linie ausdehnt. Wir können, wenn wir dies beachten, nicht sagen, daß der Fortgang der Wärme - als Kurve jetzt gedacht, nicht im Raum — wirklich etwas anderes als versinnbildlicht ist durch diese Kurve, die ich hier aufgezeichnet habe (siehe Zeichnung). Ich fasse nicht den ganzen Vorgang der Wärme durch diese Kurve ins Auge. Da ist noch irgend etwas anderes im Spiel als dasjenige, was ich durch diese Kurve ins Auge fassen kann. Und das, was da im Spiel ist, das muß die ganze Natur und Wesenheit desjenigen ändern, was ich eigentlich durch diese Kurve abbilde, welche ich als Symbolum gebrauche für die Darstellung des Wärmezustandes, gleichgültig ob ich sie geometrisch oder arithmetisch fasse.
[ 11 ] Wir haben also das Eigentümliche hier, daß, wenn wir durch unsere landläufigen geometrischen Linien erfassen wollen den Wärmezustand, insofern er durch die Temperatur zum Vorschein kommt, wir ihn nicht voll erfassen können. Das aber hat eine andere Wirkung. Denken Sie sich einmal, Sie haben eine Linie (siehe Zeichnung). Diese Linie hat eine bestimmte Länge \(l\). Erheben Sie diese Linie zum Quadrat, so können Sie dieses \(l^2\) aufzeichnen durch diese Quadratfläche.

[ 12 ] Nehmen Sie an, Sie bilden \(l^3\), so können Sie sich diese dritte Potenz aufzeichnen durch den Würfel, durch den Raumkörper. Aber nehmen Sie an, ich bilde die vierte Potenz \(l^4\), was soll ich denn jetzt tun, wenn ich weiterzeichnen will? Ich kann von der Linie zur Fläche, von der Fläche zum Körper übergehen, aber was kann ich denn jetzt tun, um zur vierten Potenz überzugehen, wenn ich nach derselben Methode weiterrücken will? Ich kann da nichts machen innerhalb unseres dreidimensionalen Raumes. Das gilt zunächst für mathematische Raumgrößen. Aber wir haben gesehen, daß der Wärmezustand, insofern er durch die Temperatur zur Anschauung kommt, gar nicht ausdrückbar ist durch Raumgrößen. Da ist noch etwas anderes drinnen. Sonst könnte ein Wärmezustand, der längs eines Stabes ist, aufgefaßt werden als bloß längs eines Stabes verlaufend. Das ist aber unmöglich. Die Folge davon ist, daß ich, wenn ich konsequent zu Werke gehe, nicht in der Lage bin, die Potenzierungen des \(t\) in derselben Weise aufzufassen, wie ich die Potenzierung der Raumgrößen auffasse. Ich bin nicht in der Lage, dasselbe zu denken über die Potenzierung des \(t\), wie ich denke über die Potenzierung des \(l\) oder irgendeiner anderen bloßen Raumgröße. Und wenn zum Beispiel — ich will das heute zunächst einmal nur hypothetisch behandeln —, wenn ich zum Beispiel nur die eine Potenz, die erste Potenz von dem \(t\) hätte, und diese nicht ausdrückbar wäre als Linie, so könnte die zweite Potenz \(t^2\) nicht ausdrückbar sein als Fläche. Und die dritte Potenz \(t^3\) könnte schon gar nicht durch eine Raumgröße ausdrückbar sein. Ich würde, wie ich bei mathematischen Raumgrößen erst aus dem Raum herauskomme, nachdem ich die dritte Potenz gebildet habe, vielleicht schon bei der zweiten Potenz aus unserem Raum herauskommen, und bei der dritten nicht mehr drinnen sein.
[ 13 ] Also denken Sie sich, Sie müßten sich das \(t\) in ganz anderer Natur vorstellen als Raumgrößen. Sie müßten das gewöhnliche \(t\) schon als etwas Quadriertes auffassen, als eine zweite Potenz, und Sie müßten das quadrierte \(t\) schon als dritte Potenz auffassen und das kubierte \(t\) als vierte Potenz, wobei Sie aus unserem gewöhnlichen Raum herauskommen. Denken Sie, dann würde diese Formel ein ganz besonderes Gesicht bekommen. Dann würde das letzte Glied, das in dieser Formel drinnen ist, mich zwingen, aus dem dreidimensionalen. Raum herauszugehen. Ich würde dann, indem ich einfach rechne, genötigt sein, mit dem letzten Glied meiner Formel aus dem dreidimensionalen Raum herauszurücken. Das sage ich jetzt rein hypothetisch, also als Möglichkeit, wie man das ja tut bei mathematischen Formeln. Nicht wahr, wenn Sie ein Dreieck betrachten und konstatieren, daß das Dreieck drei Winkel hat, so haben Sie zunächst ein gedachtes Dreieck. Weil das Denken zu bequem ist, zeichnen Sie es sich auf, um es zu versinnlichen. Aber die Zeichnung hat damit nichts zu tun. Sie haben gegeben: Die Summe der Winkel ist 180°. Oder: In einem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse gleich der Summe der Quadrate über den beiden Katheten. Das ist etwas, was man zunächst eben behandelt, wie ich jetzt das \(t\) in seiner Potenz behandelt habe. Jetzt gehen wir zurück und sehen uns dasjenige an, was wir als Erscheinung konstatiert haben. So macht man es ja in der Geometrie: Wenn ich an einer Brücke oder sonstwo nötig habe, ein Dreieck zu beobachten, so verifiziert sich das, was ich am abstrakten Dreieck gedacht habe. Was ich am abstrakten \(t\) gedacht habe, das hat zunächst — wir wollen der Wirklichkeit immer näher auf den Leib rücken, aber schrittweise — eine gewisse Ähnlichkeit mit dem, was dargestellt ist beim Schmelzen und Verdampfen. Ich war nicht imstande, das Schmelzen und Verdampfen in die drei Raumdimensionen hineinzukriegen. Die kann ich nur hereinkriegen, indem ich aufhöre, die Kurve zu ziehen, und sie dann wiederum fortsetze. Wenn nun die Voraussetzungen zutreffen, die ich vorhin machte, dann wäre ich auch genötigt, bei der dritten Potenz, bei dem Kubus der Temperatur, aus dem dreidimensionalen Raum hinauszugehen.
[ 14 ] Sehen Sie, da habe ich Ihnen einen Weg gezeigt, der in einer gewissen Weise eingeschlagen werden muß, wenn man versuchen will, die Erscheinungen, die sich dem Wärmewesen gegenüber zeigen, einfach zusammenzustellen, um durch diese Zusammenstellung etwas Ähnliches zu gewinnen wie im vorhergehenden Kursus für die Betrachtung des Lichtwesens. Von ganz anderen Voraussetzungen ist der Physiker Crookes ausgegangen. Und merkwürdig ist, daß er durch seine Erwägungen immerhin zu einem ähnlichen Resultat gekommen ist wie das, was wir jetzt bloß hypothetisch hingestellt haben, dessen Wirklichkeit wir dann zu Leibe rücken werden in den nächsten Betrachtungen. Auch er kommt dazu, die Veränderungen der Temperatur überhaupt als etwas zu betrachten, was zu tun hat mit einer Art vierten Dimension des Raumes. Es ist heute wichtig, auf diese Sache hinzuweisen aus dem Grunde, weil ja die Relativisten, Einstein an der Spitze, indem sie über die drei Dimensionen des Raumes hinausgehen, sich genötigt sehen, zur Zeit überzugehen und diese als vierte Dimension zu bezeichnen, so daß man in den Einsteinschen Formeln überhaupt als vierte Dimension die Zeit bezeichnet findet, während Crookes sich genötigt fand, als die vierte Dimension die Ab- oder Zunahme des Wärmezustandes anzusehen. Das als eine historische Einschiebung.
[ 15 ] Zu diesen Erscheinungen bitte ich Sie jetzt dasjenige zu nehmen, was ich auch früher erwähnt habe. Ich habe gesagt: Einen gewöhnlichen festen Körper kann ich hinlegen, er wird seine Form behalten, das heißt, er hat einen bestimmten Umriß. Einen flüssigen Körper muß ich in ein Gefäß hineinlaufen lassen. Er bildet immer eine Niveaufläche und nimmt im übrigen die Form des Gefäßes an. So ist es nicht beim gas- oder dampfförmigen Körper. Der dehnt sich nach allen Seiten aus. Ich muß, um ihn zu begrenzen, ihn in ein allseitig geschlossenes Gefäß einfassen. Dieses allseitig geschlossene Gefäß gibt ihm seine Form, so daß ich bei einem Gas eine Form nur habe, wenn ich es allseitig einschließe.
[ 16 ] Wenn ich einen festen Körper habe, so hat er seine Form eben dadurch, daß er ein fester Körper ist. Er hat sie gewissermaßen von selbst. Ich lasse die Flüssigkeit als Zwischenzustand jetzt aus und will als die Gegensätze den festen und den gasförmigen Körper beschreiben. Der feste Körper versorgt sich gewissermaßen selbst mit dem, was ich beim gasförmigen zufügen muß: die Wandung von allen Seiten. Nun tritt aber beim Gas etwas Besonderes auf. Wenn Sie ein Gas, statt daß sie es da drinnen haben, in ein kleineres Gefäß einschließen — dieselbe Gasmenge, dadurch daß Sie von allen Seiten die Wand zusammendrücken -, so müssen Sie eben drücken, müssen Druck ausüben.

[ 17 ] Das heißt nichts anderes als: Sie müssen den Druck des Gases überwinden. Sie haben es zu tun an den Wänden, die die Formung bilden, mit einem Druck. Wir können also sagen: Ein Gas, welches das Bestreben hat, nach allen Seiten davonzulaufen, das wird durch den Widerstand der Wände zusammengehalten. Dieser Widerstand ist von selbst da, indem ich einen festen Körper habe. So daß ich, indem ich gar nichts theoretisiere, sondern einfach den ganz gewöhnlichen Tatbestand ins Auge fasse, einen polarischen Gegensatz von Gas und festem Körper so definieren kann, daß ich sage: Dasjenige, was ich von außen hinzufügen muß beim Gas, ist beim festen Körper von selber da. Aber nun können Sie, indem Sie das Gas abkühlen, zurückgehend wiederum zum Siedepunkt, aus dem Dampf die Flüssigkeit gewinnen; indem Sie weiter abkühlend zurückgehen bis zum Schmelzpunkt, können Sie aus der Flüssigkeit wiederum die festen Körper gewinnen. Das heißt, Sie können einfach durch Vorgänge, die zusammenhängen mit dem Wärmewesen, das hervorrufen, daß Sie nicht mehr nötig haben, von außen die Formung zu bilden, sondern daß die Formung sich von innen von selbst bildet. Da ich nichts anderes getan habe, als den Wärmezustand zu verändern, so ist es ja selbstverständlich, daß diese Formung irgendwie mit der Änderung des Wärmezustandes zusammenhängt. Beim festen Körper ist etwas da, was beim gasförmigen noch nicht da war. Wenn wir dem festen Körper entgegenhalten irgendeine Wand, drückt der feste Körper auf diese Wand zunächst nicht, wenn wir nicht selber andrücken. Wenn wir dem Gas entgegenhalten eine feste Wand, drückt das Gas immer auf die feste Wand. Sie sehen, wir kommen da zu dem Begriff des Druckes und müssen dieses Entstehen des Druckes in Zusammenhang bringen wiederum mit dem Wärmezustand. Wir müssen also sagen: Es muß aufgesucht werden eine bestimmte Beziehung zwischen der Formung des festen Körpers und dem Entgegenwirken durch den Wändedruck gegen das allseitige Zerfließen des Gases. Wenn wir diese Beziehungen aufsuchen, können wir hoffen, in das Wesen des Zusammenhanges zwischen der Wärme und den Körpern wirklich einzudringen.
Third Lecture
[ 1 ] Today, in order to approach the goal we must already be nearing in the first days of our considerations, we will look at a few more phenomena concerning the relationship of the heat entity to the so-called aggregate state, that is, to what, as I told you yesterday, was referred to in the old physical worldview as earth, water, and air. You know that earth, water, air, or, as we call them today, solid, liquid, and gaseous bodies, can be transformed into one another. However, a very special phenomenon becomes apparent in relation to the heat entity. I will first describe the phenomenon, and then we will simply state it: If we take any solid body and heat it, it becomes warmer and warmer until it reaches a point where it changes from a solid to a liquid state. Now, if we use a thermometer, we can observe how the thermometer rises as the body gets warmer and warmer. At the moment when the body begins to become liquid, i.e., to melt, the thermometer stops rising. It waits until the entire body has become liquid, and only rises again within the liquid that has become of the body. So we can say that during the melting process, the thermometer shows no rise in temperature. However, we must not believe that the heat itself is not involved. If we did not supply any heat, the melting would stop. We must therefore supply heat in order to cause melting, but this heat is not shown on the thermometer; rather, heat only begins to show on the thermometer once melting is complete and the liquid that has emerged from the solid body is further heated. These phenomena must first be considered carefully. For you see that these phenomena cause an interruption in the rise of the temperature. Let us compile a number of such phenomena, which will then lead us to an understanding of the nature of heat without resorting to any imagined theories. We have prepared this solid substance, sodium thiosulfate. We will melt this substance. You can see here a temperature of about 25°. Now we are going to apply heat to this substance, and I would ask someone to come up here as a delegate to see how the temperature does not actually rise during the melting of this substance. (In the meantime, the thermometer has risen to 48°, the melting point of sodium thiosulfate, and it has melted.) Now the thermometer rises rapidly because the melting is complete, whereas before it remained steady throughout the entire melting process.

[ 2 ] Now let's try to visualize this process. We can do this in the following way. Let's think of the rise in temperature as a line that rises in this way. Let's assume that we have reached the so-called melting point with the rising temperature. Here, the body begins to melt. The temperature remains constant, as shown by the thermometer. If I continue to heat it, the temperature rises again. We would see that the liquid expands as a result of the rise in temperature, i.e., the addition of more heat. Now we continue to heat this body, which has become liquid. The temperature rises again, starting from the same point at which it was during melting (dotted line). It rises as long as the body remains liquid. We can reach a second point at which the liquid begins to boil and evaporate. We see the same phenomenon again: the thermometer stops showing an increase in temperature until the liquid has evaporated. At the moment when the liquid has evaporated, if we could hold the thermometer in the vapor, we would again see the thermometer rise (dotted line). Here, you could observe again that the thermometer does not rise during evaporation. So here I have a second limit at which the thermometer reading stops rising.
[ 3 ] Now, to this phenomenon that I have just demonstrated to you, I would like you to add another that you may be very familiar with from everyday life: if we take the solid body that formed our starting point, it is, as you know, such that it retains its shape by itself (1).

[ 4 ] If I place any solid body here, it remains as it is. If you take a liquid, that is, something that has passed through its melting point when heated, you know that I cannot place a liquid piece by piece, but I have to keep it in a vessel, and it remains in the shape of the vessel and forms a horizontal level surface at the top (2). If I take a gas, steam that has passed through the boiling point, I cannot keep it in such a container. It will escape. I can only keep such steam in a container that is closed on all sides, otherwise the steam will escape in all directions (3). At least, that is the case at first glance, and we will start from this superficial observation. And now I ask you to consider the following with me. We make these considerations in order to ultimately be able to arrive at a kind of understanding of the nature of heat by bringing them together. How did I actually establish the rising temperature? I established it through the expansion of mercury. This expansion of mercury took place in space. And even though mercury is a liquid at our average temperature, we must be aware that, even though it is held together in the vessel, the expansions in the three dimensions add up, and we only see the expansion in one direction. With the expansion of mercury in the three dimensions, we have reduced this to only one dimension, so that we observe the rise in temperature through the expansion of a body.

[ 5 ] Let's start from this observation, which we have taken as our basis, and look at the following: Let's take a line (see drawing) — of course, you can only imagine a line — and say that there are a number of points on this line, \(a\), \(b\), \(c\), \(d\), and so on. If you want to reach these points, you can certainly stay on this line. For example, if you are standing here \((a)\), you can reach point \(c\) by walking along the line. You can walk back and reach point \(a\) again. In short, if I want to reach points \(a\), \(b\), \(c\), \(d\), I can certainly stay on the line. The situation is different if we consider point \(e\) or point \(f\). You cannot stay on the line if you want to reach point \(e\) and point \(f\). You have to leave the line to reach point \(e\) and point \(f\). So you have to walk along the line somehow and then step off the line to reach these points.

[ 6 ] Now suppose you are looking at a surface, say the surface of the blackboard, and I mark a number of points on the surface of the blackboard: \(a\), \(b\), \(c\). To reach these points, you can stay on the surface of the blackboard. If you are here \((\times)\), you can travel to each of these points without ever leaving the blackboard. However, if you want to stay on the blackboard, you cannot reach this point here (in front of the blackboard), which represents another point. To do so, you must leave the blackboard. In this way, it is possible to get an idea of the dimensionality of space by saying to yourself: For points that lie in the first dimension, it is possible to reach them through this one dimension. However, for points that lie outside this one dimension, you cannot reach them without leaving this dimension. Similarly, you cannot reach points that lie in the third dimension by traversing the surface. What happens if I only talk about points \(e\) and \(f\) in relation to the one dimension in which points \(a\), \(b\), \(c\), \(d\) lie? Imagine a being that is only able to observe a single dimension and has no mental image of a second and third dimension. Such a being would move only in the one dimension, just as you move in three-dimensional space. The moment this being takes point \(a\) (see drawing) to here \((b)\) and the point then deviates and goes to \(e\), the content of this point would simply disappear for this being. It is not there for such a being, which could only perceive in such a dimension, the moment it leaves this one dimension. Similarly, all points that lie outside the two dimensions of the surface are not there for a being that can only perceive in the two dimensions of the surface. And if a point that lies in the surface decides to leave the surface, this being would have no means of pursuing this point further. It would disappear from the realm of its space. Such a being, a being that could only perceive in a single dimension, what kind of geometry would it have? It would only have a one-dimensional geometry. It would only be able to talk about distances and the like and their laws within that one dimension. A being that can only perceive in two dimensions would only be able to talk about the laws of flat figures and would only have a two-dimensional geometry. We humans initially have a three-dimensional geometry. A being with a one-dimensional geometry would have no way of somehow comprehending geometrically what a point does when it leaves the one dimension. A being with two-dimensional geometry would have no way of following what a point does when it leaves the two dimensions and is then there (in front of the blackboard). We humans—I say it again—have three-dimensional geometry. Now, since I have to do it, as I said earlier, with the expansion of mercury in three dimensions, which are reduced to only one dimension, I could, as I have done here, only by means of the blackboard, draw a line in two dimensions, or I could also draw it in such a way that I relate it to a spatial coordinate system. I would have an abscissa axis, an ordinate axis, and a third axis perpendicular to it, and I would be able to draw this line as a spatial line. The moment I arrive at either the melting point or the boiling point, I am unable to continue drawing this line in any way.

[ 7 ] Theoretically, hypothetically speaking, there would be a way to continue. Let's assume that I could do it this way: Let's say that the rise in temperature is represented by this line (see drawing). I would then have to change something else here, while keeping all other factors the same, and could then continue from another point above. That would give me another reference point for staying in my world. But I don't have such a point of reference. Because when I draw this temperature curve, I simply have to start from the same point at which the temperature stands after the body in question has melted or evaporated ( \(x\) \(x\) in the drawing), from the same point at which it arrived when the melting or evaporation began. You can see from this that, with melting point and boiling point, I am simply forced into something that cannot be compared to anything other than the situation in which a one-dimensional being finds itself when a point disappears from its one dimension into the second dimension, or a two-dimensional being when a point disappears into the third dimension. When the point comes back in and continues from the same place, i.e., when the point a is carried away to here (see drawing), goes out, and now we wait and the point comes back again, I have to continue to follow its course from the same place in the one dimension inside. Purely in terms of appearance, when the heating disappears at the melting point and boiling point, I have nothing else before me but that my temperature curve is interrupted and I must continue it from the same point after some time. But what happens to the heat during the interruption also falls outside the range in which I draw my curve — and I say explicitly I can draw it as a spatial curve. First of all — and I say first of all — there is an analogy between this disappearance of point a from the first into the second dimension and what happens to the heat indicated by the thermometer while the thermometer stands still at the melting point and boiling point.

[ 8 ] Now it is a matter of relating this phenomenon to another. You see, everything depends on this relating of phenomena; not on devising some theories, but on bringing the phenomena together so that they illuminate and explain each other. This is the difference between Goethe's physics and the physics that prevails today: Goethe's physics simply juxtaposes phenomena so that they illuminate each other, while today's physics, if it dares to venture into theories at all, seeks to theorize and fantasize about phenomena. For atoms and molecules are essentially nothing more than inventions and fantasies added to phenomena.
[ 9 ] Let us therefore consider another phenomenon together with the disappearance of the warming that can be observed by the thermometer during melting. This other phenomenon confronts us when we consider yesterday's formula:
$$V=V_o(1 + 3 \alpha t + 3 \alpha^2 t^2 + \alpha^3 t^3)$$
[ 10 ] Yesterday, I said that you should pay particular attention to the last two terms of this formula. It is particularly important for us today to consider \(t^3\) once, the third power of temperature. Take a normal spatial dimension. With this normal spatial dimension, if it is a mathematical body, you speak of length, width, and height. These are essentially the three spatial dimensions. Now, when we heat a rod, as we did yesterday, we can observe the expansion of this rod. We can also observe the temperature of this rod. But there is one thing we cannot bring about: that the rod, while it expands, does not give off heat to its surroundings, that it does not emit or radiate heat. We cannot prevent that. It is impossible for us to imagine thermal expansion—please pay attention to the word—in only one dimension. We can imagine pure spatial expansion—as is always done in geometry—in one dimension, namely as a line, but we can never even imagine a state of heat that expands only along a line. If we bear this in mind, we cannot say that the progression of heat—now thought of as a curve, not in space—is really anything other than symbolized by this curve that I have drawn here (see drawing). I do not grasp the whole process of heat through this curve. There is something else at play here besides what I can grasp through this curve. And what is at play here must change the entire nature and essence of what I am actually depicting through this curve, which I use as a symbol for representing the state of heat, regardless of whether I grasp it geometrically or arithmetically.
[ 11 ] So we have the peculiar situation here that if we want to grasp the state of heat, as it appears through temperature, using our conventional geometric lines, we cannot grasp it fully. But this has another effect. Imagine you have a line (see drawing). This line has a certain length \(l\). If you square this line, you can record this \(l^2\) by this square area.

[ 12 ] Suppose you form \(l^3\), then you can represent this third power by drawing a cube, a three-dimensional shape. But suppose I form the fourth power \(l^4\), what should I do now if I want to continue drawing? I can move from the line to the plane, from the plane to the solid, but what can I do now to move to the fourth power if I want to continue using the same method? I can't do anything within our three-dimensional space. This applies first and foremost to mathematical spatial dimensions. But we have seen that the state of heat, insofar as it is visualized by temperature, cannot be expressed by spatial dimensions. There is something else involved. Otherwise, a state of heat that is along a rod could be understood as merely running along a rod. But that is impossible. The consequence of this is that, if I proceed consistently, I am not able to conceive of the powers of \(t\) in the same way as I conceive of the powers of spatial dimensions. I am not able to think the same about the power of \(t\) as I think about the power of \(l\) or any other mere spatial dimension. And if, for example—I want to treat this hypothetically for now—if I only had the one power, the first power of \(t\), and this could not be expressed as a line, then the second power \(t^2\) could not be expressed as an area. And the third power \(t^3\) could certainly not be expressed by a spatial quantity. Just as with mathematical spatial quantities, I would only leave space after forming the third power, but with the second power I might already leave our space, and with the third I would no longer be inside it.
[ 13 ] So you have to imagine \(t\) as something completely different in nature from spatial dimensions. You would have to conceive of the ordinary \(t\) as something squared, as a second power, and you would have to conceive of the squared \(t\) as a third power and the cubed \(t\) as a fourth power, whereby you would leave our ordinary space. Think about it, then this formula would take on a very special appearance. Then the last term in this formula would force me to leave three-dimensional space. By simply calculating, I would then be compelled to move out of three-dimensional space with the last term of my formula. I am saying this purely hypothetically, as a possibility, as one does with mathematical formulas. Isn't it true that when you look at a triangle and state that the triangle has three angles, you first have an imaginary triangle? Because thinking is too convenient, you draw it down to make it tangible. But the drawing has nothing to do with it. You have given: The sum of the angles is 180°. Or: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two cathetus. This is something that you initially treat in the same way as I have now treated \(t\) in its power. Now we go back and look at what we have established as a phenomenon. That's how you do it in geometry: if I need to observe a triangle on a bridge or somewhere else, it verifies what I thought about the abstract triangle. What I thought about the abstract \(t\) initially has—we always want to get closer and closer to reality, but step by step—a certain similarity to what is represented in melting and evaporation. I was unable to fit melting and evaporation into the three spatial dimensions. I can only do that by stopping the curve and then continuing it again. If the assumptions I made earlier are correct, then I would also be forced to leave three-dimensional space at the third power, at the cube of temperature.
[ 14 ] You see, I have shown you a path that must be taken in a certain way if one wants to try to simply compile the phenomena that appear in relation to the nature of heat, in order to gain something similar to what we gained in the previous course for the consideration of the nature of light. The physicist Crookes started from completely different premises. And it is remarkable that his considerations have nevertheless led him to a similar result to what we have now merely put forward hypothetically, the reality of which we will then tackle in the next considerations. He, too, comes to regard changes in temperature as something that has to do with a kind of fourth dimension of space. It is important to point this out today because relativists, Einstein at the forefront, in going beyond the three dimensions of space, feel compelled to move on to time and designate it as the fourth dimension, so that in Einstein's formulas time is designated as the fourth dimension, while Crookes felt compelled to regard the decrease or increase in heat as the fourth dimension. That is a historical aside.
[ 15 ] Regarding these phenomena, I would now ask you to consider what I mentioned earlier. I said: I can lay down an ordinary solid body and it will retain its shape, that is, it has a definite outline. I must pour a liquid body into a vessel. It always forms a level surface and otherwise takes on the shape of the container. This is not the case with gaseous or vaporous bodies. They expand in all directions. In order to limit them, I must enclose them in a container that is closed on all sides. This container, closed on all sides, gives them their shape, so that I only have a shape for a gas if I enclose it on all sides.
[ 16 ] If I have a solid body, it has its shape precisely because it is a solid body. It has it, so to speak, by itself. I will now leave out the liquid as an intermediate state and describe the solid and gaseous bodies as opposites. The solid body provides itself, as it were, with what I have to add to the gaseous body: the wall on all sides. But now something special happens with gas. If you enclose a gas in a smaller vessel instead of having it inside, the same amount of gas, by pressing the wall together on all sides, you have to press, you have to exert pressure.

[ 17 ] This means nothing other than that you have to overcome the pressure of the gas. You are dealing with pressure on the walls that form the shape. So we can say: a gas that tends to escape in all directions is held together by the resistance of the walls. This resistance is there by itself because I have a solid body. So that, without theorizing at all, but simply considering the very ordinary facts, I can define a polar opposition between gas and solid body in such a way that I say: What I have to add from outside in the case of gas is already present in the solid body. But now, by cooling the gas, returning to the boiling point, you can extract the liquid from the vapor; by continuing to cool it back down to the melting point, you can obtain the solid body from the liquid. This means that, simply through processes related to heat, you can bring about a situation in which you no longer need to form the shape from outside, but rather the shape forms itself from within. Since I have done nothing other than change the state of heat, it goes without saying that this formation is somehow related to the change in the state of heat. In the solid body, there is something that was not yet present in the gaseous body. If we hold up any wall to the solid body, the solid body does not initially press against this wall unless we ourselves press against it. If we hold a solid wall against the gas, the gas always presses against the solid wall. You see, we arrive at the concept of pressure and must relate this emergence of pressure back to the state of heat. So we have to say: we must look for a certain relationship between the formation of the solid body and the counteracting effect of the wall pressure against the gas flowing in all directions. If we look for these relationships, we can hope to really penetrate the essence of the connection between heat and bodies.

