Second Scientific Lecture-Course:
Warmth Course
GA 321
12 March 1920, Stuttgart
Lecture XII
[ 1 ] The experiments we had anticipated carrying out today we will unfortunately have to postpone until tomorrow. At that time they will be arranged so as to show you what is necessary if I am to prove to you all that I wish to prove. Today, therefore, we will consider some things which, together with the experiments of tomorrow, will enable us to bring our observations to a conclusion the following day.
[ 2 ] As a help toward the understanding of the being of heat, I wish to call your attention to a certain fact. This fact is one which we must take into account in developing our ideas on this subject, and it is that there is a certain difficulty in understanding what is really involved in a transparent body. I am not now speaking of transparency in connection with heat. You will see, however, when we have finished that we can get helpful ideas for understanding heat from the realm of light.
I said there was a certain difficulty in understanding what a relatively transparent body is and what an opaque body is as these reveal themselves under the influence of light. I have to express myself in a different way from that ordinarily used. The ordinary method of expression in physics would be as follows: an opaque body is one that by some peculiar property of its surface reflects the rays of light that fall on it and thus become a visible body. I cannot use this form of expression because it is not a reflection of the facts, it is a statement of a preconceived theory and is not by any means to be taken as self-evident.
For to speak of rays, of light rays, is theoretical. I have dealt with that in my former course. What we meet in reality is not light rays, but an image and it is this we must hold firmly in mind. As a matter of fact, we cannot simply say: a transparent body is one that by virtue of its inner molecular properties passes light through, and an opaque body is one that throws the light back. For how can such a theory be substantiated? Recollect what I have said to you about the relations of the various realms of reality. We have solids, fluids, gaseous bodies, heat, \(x\), \(y\), \(z\) and below the solid and bordering on it the \(U\) region, and you can see that the light realm must have a relation to heat and so also must the realm of chemical activity. On the other side that which we meet, so to speak, as the fluid nature in heat or in gases must have a relation to the essence of tone. For tone appears alone with the occurrence of condensation and rarefaction in gases or aeriform bodies. [ 3 ] We may therefore suspect that where we have assumed \(x\), \(y\), \(z\), we will find the essence of light. Now the question is whether we have to look for the explanation of transparency of certain bodies is not to be immediately derived from the nature of light, nor from the relation of light to these bodies.
[ 4 ] We have the \(U\) region and this \(U\) region must have a relation to the solids on the surface of the earth. We must first ask the question and seek to apply the answer to this question to our consideration of these things. What influence has the \(U\) region on solids and can we from the nature of this influence derive anything that will show use the difference between transparent bodies and the ordinary non-transparent metals? This question must be considered and the answer to it will appear when we extend further our ideas of yesterday in regard to heat by the addition of certain other conceptions.
[ 5 ] Note now, the warmth phenomena naturally are considered as belonging to the realm of physics. Such things as conduction have been included, thought of in the way I have described to you. This spreading of heat through conduction or flow of the heat condition either through a body or from one body to another one touching it has been observed. The flow has been conceived of as though a kind of fluid were involved, and the picture is of a liquid flow. It may be compared to something readily observable in the objective world, namely the water in a brook which is at one point now, and a moment later is at a distant point. Thus is pictured the flow of heat from one spot to another when the so-called conduction of heat takes place. The phenomenon are to be found in Fourrier (other investigators might also be cited.) Let us consider these a little from our own point of view and see if we can establish their validity.
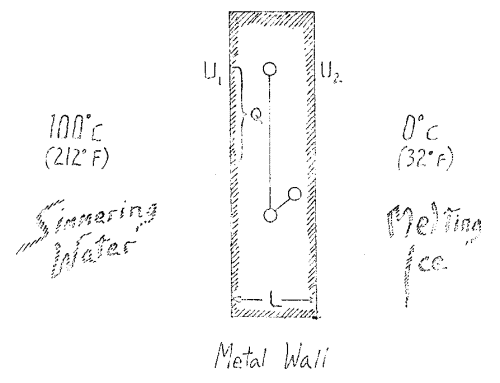
Imagine that we have a body bounded by a definite wall, say of metal (Fig. 1). Assume the wall to extend indefinitely above and below, and suppose it to consist of some sort of metal. Let us place boiling water in contact with the wall on one side holding it at a temperature \(U_1\) which in this case is \(100°C\). On the other side we place melting ice to hold the wall at a temperature \(U_2\) which in this special case will be \(0°C\)
Considering the entire phenomenon you will see that we have to do with a difference, here \(U_1\), here \(U_2\) and \(U_1\) and \(U_2\) gives us the temperature difference. Upon this difference depends the fact that we have a conduction of heat. Obviously, this transfer of heat will proceed otherwise when the difference is small, a small quantity of heat is transferred to attain equilibrium, and when the difference is great a larger quantity is transferred. Thus I may say that the quantity of heat needed to attain a certain condition depends on this temperature difference, \(U_1 - U_2\). Furthermore, it will depend not only on the difference \(U_1 - U_2\), but on the thickness of the wall which I may denote by \(l\), becoming greater when this is large and less when it is small. That is, the amount of heat transferred is inversely proportional to \(l\). I may calculate for a given area that I will call \(q\), how much heat I will need to get a certain degree of conduction. The greater \(q\) is, the greater will be the amount. Thus the amount of heat is directly proportional to \(q\) and I must multiply by this factor.
Finally, the whole process is dependent upon time. A greater effect is produced by permitting a given amount of heat to act for a longer time, a smaller effect in a less time. Therefore I have to multiply by the time. Obviously then, I must multiply through by a constant representing the heat itself, by something involving heat, since none of the quantities so far mentioned include the heat and thus cannot by themselves give the quantity of heat, \(w\), which I wish to secure. This quantity of heat, \(w\), is directly proportional to \(l\). Now if you equate all the other factors with \(U_1\) and \(U_2\), you are expressing what really flows and this not a heat quantity, essentially, nor dependent directly on a heat quantity, but is a temperature fall, a difference in level. Please keep this in mind. Just as when we pour water through a sluice and turn a paddle wheel, and the motion is due to the energy arising from a different in level, so there we have to do with a drop from one level to another, and it is this we must keep our attention on.
[ 6 ] Now we have to take up another consideration of Fourrier's to draw nearer to the being of heat. We will work over the ordinary concepts as it were so as to move nearer to reality than the physicists of the 20th century. So far I have taken into consideration only what pertains to the conducting of heat from one spot to another, but I can assume that something goes on in the body itself. Let me now ask a question. Suppose we assume that the progress of heat instead of being uniform from left to right was non-uniform, then the formula would have to apply to the inner lack of uniformity. If the irregularity in the partition of heat is present I must bring it into my considerations in some way. I must bring in the differences that reveal themselves within, that is, what takes place in the body as the temperature effects equalize themselves. As you can easily see, my formula is applicable to the process. I can say
$$w = \frac{U_1-U_2}{l} \cdot t \cdot c \cdot q.$$
That represents what takes place here. I will not consider the whole thickness of the wall, but deal with small portions of it, and will consider what happens in these small portions, as over the entire distance it is expressed by the factor \(\frac{U_1-U_2}{l}\) It is thus a question of dealing with minute distances within the body. To do this, I employ the differential ratio \(d \ u\) where \(\frac{d \ u}{d \ x}\) represents an infinitesimal movement of heat. If this is considered for an instant of time, I must multiply by \(d \ t\), this being left out of account if I do not consider the time. Thus we have \(w\) as an expression of the quantity of heat transferred through small distance in order to equalize the temperature within the body. The following formula expresses the effects of temperature fall within the body:
$$w=c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (1)$$
[ 7 ] In relation to this, I will ask you please to consider what we took up yesterday in a sketchy way, which will be clearer tomorrow when we have carried out the necessary experiments. Today, I will simply mention it, since we must keep it in mind. I refer to the relation between heat, light and chemical effect in the spectrum. Yesterday, your attention was called to the following fact: when we have an ordinary terrestrial spectrum, in the middle is the light effect proper, towards one end (Fig. 2, arrow) heat effects, toward the other end the chemical effects Now we have to consider the following.
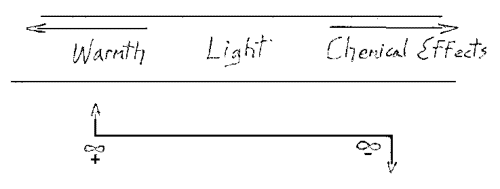
[ 8 ] We have seen that when we construct a picture of this spectrum, we must not think of light, heat and chemical effects as stretched out in a straight line. We go toward the left to approach the warm end of the spectrum and toward the right to approach the chemically active end. (Fig. 2) thus, it is not possible to remain in the lane of the pure light effects if we wish to symbolize the heat effects; nor can we remain in this place if we wish to symbolize the chemical effects. We have to move out of this plane.
Now to visualize the whole matter, let us make clear to ourselves how we must really represent a heat quantity working within a body by means of our formula. How must we represent qualitatively the relation between it and the chemical effect? We will not do this properly until we take into account the fact that we go one way to reach the heat and the opposite way to reach the chemical effects. This fact must be kept in mind if we would orient ourselves. So when we consider W as a positive quantity here (or we might consider it negative) then we have to consider the corresponding chemical effect as:
$$w=-c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (2)$$
The foregoing equation corresponds to the chemical effect, and this one:$$w=+c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t$$ corresponds to the heat effect.
[ 9 ] As a matter of fact, these things demonstrate for us an important point. This point is that when we use formulae we cannot handle the mathematical quantities merely as such if we at the same time expect the formulae to express the relations within a field of actual effects, an observed realm, where heat and chemical action are manifesting themselves. In ordinary combustion, for instance, where we wish to bring heat and chemical effects into relation, we must, if we use formulae, set down as positive what represents heat and as negative what represents chemical effect.
[ 10 ] Now if you carry your considerations further, you may make the following statement: When we think of heat as extending in one direction, so to speak, and chemical action as extending in the opposite, then we have what is essential in light left in a plane at right angles to the imagined chemical action-heat lines and between them. But if you have reserved positivity for heat and negativity for chemical action, you cannot use either of these for light effects. At this point you have to apply to the light effects a set of facts which today are only vaguely felt and not by any means explained, namely the relation between positive and negative numbers and imaginary numbers. When you are dealing with light phenomena you have to say:
$$w=\sqrt{-1} \cdot c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (3)$$
[ 11 ] That is to say, if you wish to deal with the relation of heat, chemical action and light working in the same phenomenological field at the same time, you have to use imaginary numbers—your calculation has to involve the mathematical relations expressed in imaginary numbers. But now we have already made the following statement. The spectral band that we can produce experimentally under terrestrial conditions is to be thought of actually as a circle that has been opened out. Furthermore, the complete spectrum has the peach blossom color above. If, by the employment of a sufficiently great force, you were able to bend the spectrum into a circle, you would bring together what apparently extends off into infinity in either direction. Now you can realize that this closing up cannot simply be thought of as being carried out in a circle in one plane. For as you go out into the heat region you also go off to one side (i.e. into something qualitatively different) and, proceeding into the chemical effect region, you go off to the other side. You are then in a situation where you must go first into the infinite on one side and then into the infinite on the other side and then into the infinite on the other side. You have first the awkward problem of going into infinity in a plane in one direction and then coming back from infinity and entering the plane on the other side. This implies that you reach the same infinite point no matter what direction you take. Moreover, you are confused unless you assume that you reach the same point as you go out in one direction and then in the other and you then have to come back from two different points at infinity. The way to discovery of the peach blossom color is thus a doubly complicated one. [ 12 ] Not only must you bend the spectrum in one plane, but at right angles with, say an electromagnet, you will have to turn the magnet. That, however, lead to another point. If the magnet would have to be turned, then none of the mathematical expressions so far given would apply entirely. [ 13 ] We then have to call in what was put before you yesterday in the discussion following the lecture by Messrs. Blumel and Strakesch, namely the super-imaginary number. You will doubtless recollect that we have to take into account that there is controversy about these super-imaginary numbers. They are readily handled mathematically and have, so to speak, more than one meaning. Some mathematicians even question whether there is any justification for them at all. Physics does not give us a definite formulation of the super-imaginary numbers. Nevertheless we put them into the series because we are led to see that they are necessary if we wish to formulate in an orderly manner what happens in the realm of chemical activity, light, heat, and what takes place in addition when we pass out in one direction through this series and come back into it from the other direction.
One who has the organ to perceive these things finds something very peculiar. He finds something which, I believe, furnishes a real foundation for illuminating the basic facts of physical phenomena. What I mean my friends, is this. The same sort of difficulty that meets one in the consideration of super-imaginary numbers also meets one when the attempt is made to apply the science of the inorganic to the phenomena of life. It cannot be done with these concepts of the inorganic. They simply do not apply. What has been the result of this? On the one hand there are thinkers who say: “The organic things of the earth have arisen by a transformation out of the inorganic.” But with this view alone one can never enter the reality of the living. Other thinkers like Prayer, regard the organic as the source of the inorganic and come nearer the truth. They think of the earth as originally a living body and what is today inorganic they consider as something thrown off or as that which has died out of the organic. But these people do not make us an entirely satisfactory picture.
The same difficulty that meets us in the phenomena of nature considered by and for themselves is met also when we attempt a comprehensive formulation of what is present in the realms of heat, light, and chemical activity and what is come upon when we attempt to close the color band in a natural manner. We must assume, of course, that this color band can be closed somewhere although it is obvious that it cannot be done under terrestrial conditions.
It is necessary for us to recognize how the purely mathematical leads up to the problem of living. With the faculties at hand today you can handle the phenomena of light, heat and chemical action, let us say, but you cannot handle what is evidently connected with these, namely the opening up of the spectrum. This cannot be formulated in a manner corresponding to the others.
[ 14 ] It will be helpful to us at this stage if we set up a terminology. We can base this terminology on rather definite concepts. We say: Something real is at the basis of the formula for W. Let us speak of this as heat ether. Likewise something real is involved when we change the positive signs of the heat formula to negative ones, and here we speak of the chemical ether. Where our formulae involve imaginary numbers, we speak of the light ether. [ 15 ] You see here an interesting parallelism between thinking in mathematics and thinking within science itself. The parallelism shows how we are really dealing not so much with an objective difficulty but rather with a subjective one. For the purely mathematical difficulty arises of itself, and independently of the science of external things. No one would think that a beautifully built lecture could be delivered on the limits of mathematical thinking, similar to the one du Bois-Reymond delivered on the limits of knowledge of nature. At least the conclusions would be different. Within mathematics, unless the matter slips us because it is too complicated, in this realm of the purely mathematical it must be possible to set up a completely formulated expression. The fact that one cannot do this hangs together with our own relative lack of maturity. It is unthinkable that we have here an absolute shortcoming or limit to human knowledge. It is extremely important that you hold this before your minds as a fundamental. For this shows us how we cannot apply mathematics if we wish to enter reality unless we keep in mind certain relations. We cannot simply say with the energeticists, for instance, “a given quantity of heat changes into a certain quantity of chemical energy and vice versa.” That we cannot do, but we must bring in certain other values when a process of this kind takes place. For the necessity of the case constrains us to see as essential not the quantitative mechanical change from one energy to another but rather the qualitative aspect of the transformation. This is indeed to be found along with the quantitative.
If people turned their attention to these qualitative changes which are expressed by the numerical formulations, such ideas as the following would not be advanced: “Apparently heat is just heat because we experience it as such, mechanical energy is as we experience it, chemical energy is what we see as chemical processes; but within, these processes are all alike. Mechanical energy is manifesting everywhere and heat is nothing but a form of this energy.”
This idea of a bombardment, of collisions between molecules and atoms or between these and the wall of the vessel—this struggle for an abstract unity of all energy which makes it into a mechanical motion and nothing more—such things as these would not have arisen if it had been seen that even when we calculate we must take into account the qualitative differences between various forms of energy. It is very interesting in this connection to see how Eduard von Hartmann was obliged to find definitions for physics that excluded the qualitative. Naturally, one cannot find this in the one-sided mathematics of physics, and aside from the cases where negative quantities arise from purely mathematical relations, physicists do not like to reckon with numerical quality differences. They use positive and negative signs, but only because of purely mathematical relationships. In the ordinary theory of energy, justification would never be found for making one energy positive and another negative on the basis of qualitative differences.
Zwolfter Vortrag
[ 1 ] Die Versuche, die wir für heute vorhatten, müssen wir leider auf morgen verschieben. Sie werden morgen so weit sein, sie so zu zeigen, wie ich sie haben muß, wenn ich das Ganze besprechen will, was gerade daran geprüft werden soll. Wir werden daher heute eine Betrachtung einschieben über diejenigen Dinge, die wir auch noch brauchen, morgen dann die Versuchsanordnungen machen, um die Betrachtungen übermorgen zu einem vorläufigen Abschluß zu bringen.
[ 2 ] Dasjenige, was ich zunächst wie eine Hilfe anführen möchte für unsere Anschauungen, die wir entwickeln müssen gegenüber dem Wärmewesen, das ist, daß ich Sie hinzuweisen habe darauf, daß eine gewisse Schwierigkeit vorliegt im Verstehen dessen, was eigentlich ein durchsichtiger Körper ist. Ich rede jetzt nicht von Wärme. Aber Sie werden sehen, namentlich wenn wir diese Versuche hinter uns haben, wie wir eine Hilfsvorstellung vom Licht aus für das Verständnis des Wärmewesens gewinnen werden. Es liegt eine gewisse Schwierigkeit vor, sage ich, zu verstehen, was ein relativ durchsichtiger Körper ist und was ein undurchsichtiger Körper ist, also ein Körper, der uns gewissermaßen sich selber unter dem Einfluß des Lichtes zeigt. Ich muß etwas anders sprechen, als gewöhnlich gesprochen wird. Die Sprache der gewöhnlichen Physik würde sagen: Ein undurchsichtiger Körper ist derjenige, der uns durch eine gewisse Beschaffenheit seiner Oberfläche die Lichtstrahlen zurückwirft, die auf ihn fallen, und der dadurch als Körper sichtbar wird. — Diese Ausdrucksformen kann ich nicht wählen, weil sie ja durchaus nicht eine Wiedergabe des Tatbestandes sind, sondern weil sie Ausdrücke sind von schon vorhandenen, bestimmten Theorien, die wir nicht ohne weiteres als selbstverständlich annehmen können. Denn von Strahlen zu sprechen, von Lichtstrahlen zu sprechen, ist Theorie. Ich habe darüber ja in meinem vorigen Kursus auch schon gesprochen. Alles dasjenige, was uns entgegentritt in der Wirklichkeit, ist nicht Lichtstrahl, sondern ist Bild, und das ist durchaus etwas, was festzuhalten ist. Außerdem können wir nicht ohne weiteres sagen: Ein durchsichtiger Körper ist derjenige, der durch seine innere molekularische Beschaffenheit das Licht durch sich durchgehen läßt, und ein undurchsichtiger Körper ist derjenige, der das Licht zurückwirft. Denn wie sollte denn eine Möglichkeit sein, eine solche Theorie ohne weiteres zu rechtfertigen? Und wenn Sie an das sich erinnern, was ich in diesen Tagen dargestellt habe als die Verhältnisse der Wirklichkeitsgebiete: feste, flüssige, gasförmige Körper; Wärmewesen; \(x\), \(y\), \(z\) und dann unter den festen Körpern angrenzend das \(U\)-Gebiet, so werden Sie sehen, daß in irgendeiner Weise mit dem Wärmegebiet in Beziehung stehen muß das Lichtgebiet, auch in Beziehung stehen muß das Gebiet der chemischen Wirkungsweisen. Auf der anderen Seite muß mit dem, was uns entgegentritt, ich möchte sagen, als die flüssige Gestalt im Wärmewesen, im Luftwesen, in irgendeiner Beziehung stehen dasjenige, was die wahre Wesenheit des Tones ist. Denn Töne erscheinen bei Gelegenheit von Verdichtungen und Verdünnungen in gas- oder luftförmigen Körpern.
[ 3 ] Wir können also zunächst vermuten, daß irgendwo da, wo wir das \(x\), \(y\), \(z\) angenommen haben, auch die Wesenheit des Lichtes gefunden werden kann. Aber es ist die Frage, ob wir da, wo wir die Wesenheit des Lichtes suchen, auch zu suchen haben zum Beispiel die Wesenheit der Durchsichtigkeit gewisser Körper. Diese Wesenheit der Durchsichtigkeit gewisser Körper ist nicht ohne weiteres aus der Wesenheit des Lichtes heraus oder nur aus den Beziehungen des Lichtes zu den festen Körpern zu suchen. Wir haben das \(U\)-Gebiet, und dieses \(U\)-Gebiet muß mit seinen Wirkungen in irgendeiner Weise ein Verhältnis haben zu festen Körpern, die an der Oberfläche der Erde sind. Und wir werden wenigstens zunächst die Frage aufwerfen müssen und noch hinarbeiten auf die Beantwortung dieser Frage in diesen Betrachtungen, die uns bei meiner Anwesenheit noch zur Verfügung stehen: Welchen Einfluß hat das \(U\)-Gebiet auf feste Körper, und kann uns nicht etwas von diesem Einfluß offenbaren der Unterschied, der auftritt zwischen durchsichtigen Körpern und den gewöhnlich undurchsichtigen Metallen? Also solche Fragen müssen uns zunächst beschäftigen. Und den Weg zur Beantwortung solcher Fragen werden wir finden, wenn wir nun versuchen, das, was sich uns gestern ergeben hat über das Wärmewesen, durch einige andere Begriffe noch zu ergänzen.
[ 4 ] Man hat ja natürlich gesehen innerhalb des Gebietes der Physik die Tatsachen, die sich ergeben als Wärmeerscheinung. Man hat eben solche Tatsachen gesehen wie die, die man unter dem Begriff der Wärmeleitung gedacht hat, die wir Ihnen ja auch vorgeführt haben. Man hat vor allen Dingen diese Art der Ausbreitung der Wärme bei der Wärmeleitung, also bei dem Fortfließen des Wärmezustandes entweder durch einen Körper oder über die Berührungsstelle hinaus durch zwei oder mehrere sich berührende Körper, beobachtet. Man hat dieses Fortfließen der Wärme sich so vorgestellt, wie wenn eine irgendwie geartete, unbestimmte Flüssigkeit, zunächst wie das Bild nur des Fortfließens der Wärme, des Wärmezustandes, da wäre. Und nun kann man schon einmal anknüpfen an das, was ja die äußere Anschauung bietet: So wie Wasser irgendwie in einem Bach fortfließt, das heißt, an einem weiteren Punkt später ist als vorher, was ja die Natur so fließend darstellt, so kann man auch folgen dem Fortfließen der Wärme von einem Punkte zum anderen, wenn die sogenannte Wärmeleitung stattfindet. Gedanken über dieses Fortfließen des Wärmezustandes im Sinne der Wärmeleitung haben sich die verschiedensten Menschen gemacht. Ziemlich klare Vorstellungen — wir könnten auch von anderen ausgehen — rühren her von Fourier, und an diese wollen wir ein wenig anknüpfen und wollen dann sehen, wie wir gegenüber den Erkenntnissen, die wir schon gewonnen haben, mit diesen Vorstellungen zurechtkommen.
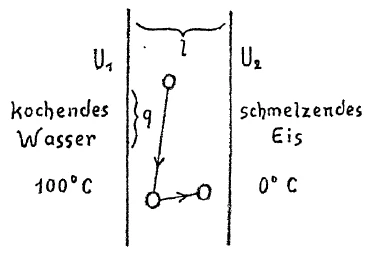
[ 5 ] Da können Sie sich vorstellen: Wir stehen einem abgeschlossenen Körper gegenüber, irgendeinem Metall, das hier scharf begrenzt wäre durch eine Ebene, und hier ebenfalls durch eine Ebene. Nach oben und unten können wir es uns ins Unbestimmte verlaufend denken. Wir versuchen dadurch, daß wir diese Grenze des Metalls in siedendem Wasser halten, sie auf einer Temperatur \(U_1\), zu halten, die etwa in diesem Falle \(100°C\) sein könnte, und versuchen die andere Grenzfläche mit schmelzendem Eis so in Berührung zu halten, daß wir eine Temperatur \(U_2\), haben, die im speziellen Fall \(0°C\) sein kann. Wir haben, wenn Sie sich den ganzen Sachverhalt vor Augen führen, es zu tun mit einer Differenz: hier \(U_1\), hier \(U_2\); \(U_1-U_2\), gibt uns eine Temperaturdifferenz. Von dieser Temperaturdifferenz wird es abhängen, wie die Wärmeleitung vor sich geht. Denn selbstverständlich, wenn die Temperaturdifferenz groß ist, so muß die Wärmeleitung anders vor sich gehen, als wenn die Temperaturdifferenz kleiner ist. Ich brauche kein großes Quantum von Wärme, wenn diese Temperaturdifferenz kleiner ist, ich brauche ein größeres Quantum von Wärme, wenn diese Differenz größer ist, um denselben Effekt zu erreichen, so daß ich also sagen muß: Die Wärmemenge, die ich brauche, um einen gewissen Effekt zu erreichen, die wird abhängen von dieser Temperaturdifferenz \(U_1-U_2\);. Sie wird weiter abhängen nicht nur von dieser Differenz \(U_1-U_2\), sondern wenn ich die Länge des Körpers mit \(l\) bezeichne, so wird die Wärmemenge, die ich brauche, um einen bestimmten Effekt zu erreichen, kleiner werden, wenn diese Länge groß ist, als wenn diese Länge klein ist. Das heißt: Im umgekehrten Verhältnis wird die Wärmemenge von \(l\) abhängig sein. Ich werde berechnen können für einen bestimmten Querschnitt, den ich als, sagen wir, \(q\) bezeichne, die Wärmemenge, die ich da brauche, um einen gewissen Effekt der Wärmeleitung zu erreichen. Je größer dieser Querschnitt ist, desto mehr Wärme werde ich brauchen, je kleiner der Querschnitt ist, desto weniger Wärme werde ich brauchen. Also steht \(q\) im geraden Verhältnis, ich werde damit zu multiplizieren haben. Dann wird endlich die ganze Sache abhängen von um der Zeit. Ich werde mit der Zeit zu multiplizieren haben. Das Ganze muß ich dann selbstverständlich, da mir alle diese Größen ja nicht ohne weiteres Wärme geben, mit irgend etwas, worin die Wärme schon steckt — denn alles das ist ja nicht Wärme — mit einer Konstanten, die das Wärmemaß darstellt, multiplizieren, mit \(c\), dann bekomme ich meine Wärmemenge \(w\). Diese Wärmemenge \(w\) also ist abhängig im geraden Verhältnis von \(U_1-U_2\), und den anderen Faktoren, im umgekehrten Verhältnis von \(.\) Sie sehen, wenn Sie in dem Zusammenhang alle anderen Faktoren mit \(U_1\), und \(U_2\), vergleichen, daß man es zu tun hat bei dem, was da eigentlich fließt, nicht direkt mit einem Wärmezustand, oder mit irgend etwas, was sich auf die Wärme bezieht, sondern mit einem Wärmegefälle, mit einem Niveauunterschied. Das bitte ich Sie, immer ins Auge zu fassen. Genau so, wie man es mit einem Niveauunterschied zu tun hat, wenn man etwa bei einer Schleuse Wasser von oben nach unten stürzen läßt und ein Schaufelrad in Bewegung setzt, und wie die Triebkraft, die da entwickelt wird, abhängt von dem Niveauunterschied, den man in Rechnung ziehen muß, so hat man es auch hier zu tun mit einem Gefälle, und das ist, was wir besonders ins Auge fassen müssen.
[ 6 ] Nun handelt es sich darum, daß wir, wenn wir dem Wärmewesen näher kommen wollen, auch noch einer anderen Erwägung von Fourier nachgehen müssen, damit wir gewissermaßen rektifizierend an diesen gebräuchlichen Vorstellungen weiterschreiten und in unseren Betrachtungen mehr der Wirklichkeit gemäß fortfahren, als es die Physiker des 19. und 20. Jahrhunderts getan haben. Ich habe jetzt eisentlich nur in Erwägung gezogen dasjenige, was geschieht bei der Fortleitung der Wärme von einem Ende des Körpers zum anderen, aber ich nehme an, daß da in den Körpern drinnen selbst noch irgend etwas vorgeht. Ich frage nun: Wenn hypothetisch die Sache so sein würde, daß nicht einfach gleichmäßig hier von links nach rechts der Wärmefortschritt geschähe, sondern im Inneren ungleichmäßig, wie müßte ich dann anwenden wiederum diese Formeln hier auf die inneren Unregelmäßigkeiten? Wenn also Unregelmäßigkeiten in der Verteilung der Wärme da wären, wenn die Wärme von hier hierher (vergleiche die Verbindungslinie im Inneren des Metalls, Zeichnung Seite 179) geleitet würde und so weiter, so müßte ich dieses innere Leiten der Wärme irgendwie in Erwägung ziehen. Ich müßte dann dasjenige in Erwägung ziehen, was an Änderungen dieser Differenzen da drinnen sich offenbart, ich müßte also in Erwägung ziehen, was in dem Körper selber an Ausgleichungen von Temperaturwirkung geschieht. Dadurch würde sich, wie Sie leicht sehen können, diese meine Formel verwandeln. Ich würde zunächst sagen müssen:
$$w = \frac{U_1-U_2}{l} \cdot t \cdot c \cdot q.$$
Jetzt habe ich es nicht mehr mit der Länge \(l\) zu tun, die hier ist, sondern ich habe es mit kleinen Strecken zu tun. Und ich will betrachten dasjenige, was ebenso auf diesen kleinen Strecken geschieht, wie es geschieht in der ganzen Breite hier durch: den Faktor \(\frac{U_1-U_2}{l}.\) Es handelt sich also darum, daß ich das für kleine Strecken \(d \ x\) darinnen betrachte. Wenn ich das tue, verwandelt sich mir dieser endliche Quotient einfach in \(\frac{d \ u}{d \ x}\) wobei du der kleine Fortschritt des Wärmezustandes sein soll. Und betrachte ich dieses für eine gewisse kleine Zeit, so müßte ich noch multiplizieren mit \(d \ t\) - ich könnte das dt zunächst auch weglassen, wenn ich von der Zeit absehe. So würden wir also in diesem w haben den Ausdruck für das Wärmequantum, das jeweils an einem Punkt, aus der Sache selbst heraus, bei innerer Arbeit der Wärme aufgewendet werden müßte, um nach allen Seiten hin etwa notwendigen Temperaturgefällen zu folgen, Temperaturgefälle auszugleichen. Sie müssen sich vor Augen stellen, daß diese Formel hier
$$w = c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (1)$$
zum Ausdruck bringen würde solche Wirkungen, die da auftreten durch die inneren Temperaturgefälle in den Körpern.
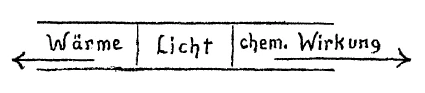
[ 7 ] Damit in Zusammenhang bitte ich Sie jetzt dasjenige zu betrachten, was wir schon gestern uns andeutungsweise vor Augen geführt haben und was uns ganz klar werden wird morgen, wenn wir die entsprechenden Versuchsanordnungen haben werden. Ich kann es trotzdem heute schon erwähnen, daß man sich vor Augen führen muß, wie auftreten die Verhältnisse des Erwärmens, des Leuchtens, des chemischen Wirkens im Spektrum. Ich habe schon gestern darauf aufmerksam gemacht: Wenn ich ein gewöhnliches irdisches Spektrum habe, habe ich in der Mitte die eigentlichen Lichtwirkungen, nach hierhin die Wärmewirkungen, nach hierhin die chemischen Wirkungen. Nun handelt es sich um folgendes: Wir haben gesehen, daß, wenn wir ein Bild entwerfen wollen für dieses Spektrum, wir gar nicht dieses Bild, das aufnehmen soll Lichtwirkungen, Wärmewirkungen, chemische Wirkungen, zu einer geraden Linie machen können. Wir müssen hier links herausgehen (aus der Ebene nach vorn), wenn wir die Linie für das Licht so ziehen (horizontal), um für die Wärme das entsprechende Symbolum zu finden. Für die chemischen Wirkungen müssen wir hierher gehen (aus der Ebene nach hinten). Es könnte auch umgekehrt sein, aber wir wollen es zunächst so festhalten.

[ 8 ] Also, wir haben keine Möglichkeit, innerhalb dieser Ebene zu bleiben, wenn wir die Wärme symbolisch umfassen wollen; wir haben keine Möglichkeit, in der Ebene zu bleiben, wenn wir die chemischen Wirkungen symbolisch umfassen wollen. Wir müssen aus der Ebene herausgehen. Und um dieses Ganze zu fassen, wollen wir das also uns klarmachen: Wie müssen wir das denn eigentlich bezeichnen, wenn wir irgendein Wärmequantum, das da wirksam ist im Inneren eines Körpers, durch diese Formel ausdrücken? Wie müßten wir das denn bezeichnen, wenn wir ein quantitativ dazu in Beziehung stehendes chemisches Quantum hätten? Wir kämen nicht zurecht, wenn wir nicht irgendwie eine Bezeichnung einführen würden, die darauf hinweist, daß wir, während wir mit der Wärme hinausgehen müssen, wir mit den chemischen Wirkungen hineingehen müssen. Wir kommen nicht zurecht, wenn wir das nicht ins Auge fassen. Wenn wir das w hier als eine positive Größe auffassen — wir könnten es auch als negative Größe nehmen -, so dürfen wir, wenn es uns darauf ankommt, nun die entsprechende Verteilung der chemischen Wirkungen zu suchen, nicht anders, als das entsprechende
$$w = - c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (2)$$
zu bezeichnen. Das entspricht den chemischen Wirkungen.
Und dieses
$$w = + c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t$$
entspricht den Wärmewirkungen.
[ 9] In der Tat, diese Erwägungen zeigen uns schon, daß wir nicht ohne weiteres bloß die Quantitäten wählen können, wenn wir Formeln schaffen wollen und wenn wir in diesen Formeln gleichzeitig ausdrücken wollen, daß wir es mit einem Beobachtungsfeld zu tun haben oder mit einem Wirkungsfeld, wo Wärme und chemische Wirkungen auftreten. Schon bei einer gewöhnlichen Verbrennung, wo wir in Beziehung bringen wollen das chemische Geschehen zu dem Wärmeeffekt, müssen wir, wenn wir durch Formeln arbeiten, einfach alles dasjenige, was wir für den Wärmeeffekt positiv einsetzen, für die entsprechenden chemischen Wirkungen negativ einsetzen.
[ 10 ] Wenn Sie nun Ihre Erwägungen weiter anstellen und sehen: Die Wärme biegt sich gewissermaßen heraus, die chemischen Wirkungen biegen sich hinein (siehe Zeichnung Seite 182), dann bleibt eigentlich nur das, was im Licht vorhanden ist, in der Ebene. Aber wenn Sie sich jetzt reserviert haben das + für die Wärme, das — für die chemischen Wirkungen, dann können Sie nicht mehr mit irgendeinem Positiven oder Negativen für die Lichtwirkungen auskommen, dann müssen Sie alles das, was Sie nur ahnen, was heute noch nicht einmal geklärt ist, das Verhältnis von positiven und negativen Zahlen zu imaginären Zahlen, anwenden auf die Lichtwirkungen, und Sie müssen, wenn Sie es mit Lichtwirkungen zu tun haben, sagen:
$$w = \sqrt{-1} \cdot c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (3)$$
Das heißt, Sie müssen hier mit imaginären Zahlen, mit mathematisch imaginären Zahlenverhältnissen rechnen, um wirklich Beziehungen zwischen Licht-, Wärme- und chemischen Effekten, die in einem gemeinsamen Versuchsfelde sind, aufsuchen zu können.
[ 11 ] Aber wir haben uns ja gesagt: Dieses Spektralband, das wir eigentlich innerhalb der Erde bilden, das ist im Grunde genommen nur der auseinandergezogene Spektralkreis, und das vollständige Spektrum würde hier oben das Pfirsichblüt haben. Wenn Sie sich durch mächtige Kräfte das Spektralband zum Kreis formen würden, würden Sie da oben bekommen den Zusammenschluß dessen, was scheinbar ins Unendliche nach links und ins Unendliche nach rechts geht. Und dieser Zusammenschluß, Sie können sich denken, daß man ihn nicht einfach durch einen Kreis bekommen kann. Denn geht man durch die Wärme, so geht man ja zugleich heraus und geht dorthin (nach vorne); und geht man durch die chemischen Wirkungen, so geht man nach der anderen Seite (nach hinten). Sie sind also jetzt in die Lage versetzt: Erstens dorthin zu gehen scheinbar ins Unendliche, und zweitens dorthin zu gehen scheinbar ins Unendliche. Sie haben nicht nur die unangenehme Aufgabe, wie bei einer Geraden dahin zu gehen (von links nach rechts) und den unendlich fernen Punkt aufzusuchen und auf der anderen Seite zurückzukommen, wenn dieser unendlich ferne Punkt (rechts) derselbe ist wie der andere (links) — da sind Sie wenigstens in einer Ebene. Aber nun irren Sie ab, gehen hierhin (links vorne) und gehen dorthin (rechts hinten) und können nicht zurückkommen, wenn Sie nicht voraussetzen, daß die Unendlichkeit hier und dort Sie an denselben Punkt führt. Aber während Sie dorthin gehen, spazieren Sie dorthin auch fort in die Unendlichkeit. Sie gehen also so, daß Sie nicht nur nach der einen Seite in die Unendlichkeit spazieren, sondern Sie spazieren auch hier hinauf (in der unteren Zeichnung Seite 182 der Pfeil links, der räumlich «vorn» bedeutet) in die Unendlichkeit und müssen von zwei Unendlichkeiten wiederum zurückkommen (entsprechend der Horizontalen und der Richtung der Pfeile). Sie gehen also einen doppelt komplizierten Weg. Dann würden Sie erst hier dieses Pfirsichblüt finden, also nicht, indem Sie einfach das zusammenbiegen, sondern indem Sie es noch außerdem im rechten Winkel abbiegen nach der einen und nach der anderen Seite.
[ 12 ] Stellen Sie sich vor, Sie würden das Farbenband mit einem Elektromagneten behandeln, so würden Sie diesen Elektromagneten auch noch drehen müssen. Das aber führt Sie dazu, zu sagen: Was Sie da finden würden, könnten Sie jetzt mit all diesen Charakteren nicht bezeichnen. Da würden Sie zu Hilfe nehmen müssen eben dasjenige, worauf gestern aufmerksam gemacht worden ist in der Diskussion: die überimaginäre Zahl.
[ 13 ] Nun wird es Ihnen ja vielleicht erinnerlich sein, daß wir hier darauf hinweisen konnten, daß diese überimaginären Zahlen strittig sind, daß man mathematisch mit ihnen nicht recht zurecht kommt, daß man sie sozusagen nicht eindeutig aufschreiben kann. Es gibt Mathematiker, die überhaupt bezweifeln, daß man ein Recht hat, von diesen überimaginären Zahlen zu sprechen. Hier führt die Physik selbst allerdings nicht gleich auf eine ordentliche Formulierung der überimaginären Zahlen, aber die Forderung dieser überimaginären Zahlen, sie führt dazu, einzusehen, daß es solcher überimaginären Zahlen bedarf, wenn man formelhaft ausdrücken will dasjenige, was erstens geschieht im Felde des Chemischen, des Leuchtenden, des Wärmewesenhaften, und was dann noch dazu geschieht, wenn wir aus dem hinausgehen und oben zurückkommen. Wer nun ein Organ dafür hat, der findet hier etwas höchst Eigentümliches. Er findet etwas, von dem ich glaube, daß, wenn man es ordentlich durchdenkt, man im Grunde genommen viel davon hat für eine sachgemäße Beleuchtung der physikalischen Erscheinungen. Das, was ich meine, ist dieses, daß man dieselben Schwierigkeiten hat, wenn man in der Naturwissenschaft das Unorganische betrachtet und von den Begriffen, die man sich innerhalb des Feldes des Unorganischen bildet, übergeht zu dem Versuch, das Leben zu begreifen. Es geht nicht mit den unorganischen Vorstellungen. Es geht nicht. Das zeigt sich auf der einen Seite dadurch, daß es Denker gibt, die sagen: Das Irdisch-Organische muß durch eine Art von Urzeugung aus dem Unorganischen hervorgegangen sein. Aber es ist unmöglich, mit dieser Anschauung zunächst irgend etwas Reales zu verbinden. Andere Denker, wie Preyer oder ähnliche, leiten alles Unorganische aus dem Organischen her, wobei sie der Wahrheit schon näher kommen. Sie denken sich die Erde als ursprünglich lebendigen Körper, und das, was heute unorganisch ist, denken sie sich wie eine Abscheidung, etwas, was herauserstorben ist aus dem Organischen. Aber über ein gewöhnliches Bild kommen auch diese Leute nicht hinweg. Dieselben Schwierigkeiten, die man da hat, wenn man auf reine Naturbegriffe geht, hat man innerhalb der Mathematik selber, wenn man versuchen will, mit gut überlegtem Formelwesen von dem, was sich erfassen läßt im Gebiete der Wärme, im Gebiete des Leuchtenden, im Gebiete des Chemischen übergehen zu wollen zu dem, was da irgendwo vorhanden ist, wo das Farbenband sich auf naturgemäße Weise schließen würde - wir müssen ja voraussetzen, dieses Farbenband wird sich irgendwo schließen: Im Bereich des Irdischen wird es sich wohl nicht schließen. Wir haben die Notwendigkeit, darauf hinzuweisen, wie die Mathematik durch ihre eigenen Erwägungen vor dem Lebensproblem steht. Sie kann mit dem, was ihr heute vorliegt, bezwingen dasjenige, was innerhalb des Lichtes, der Wärme, des Chemischen gelegen ist, sie kann nicht bezwingen dasjenige, was wir offenbar damit verbunden finden: den Abschluß des Spektrums, welcher aber nicht durch solche Formeln zum Ausdruck zu bringen ist, wie das andere.
[ 14 ] Zunächst helfen wir uns dadurch, daß wir einfach eine Terminologie gebrauchen. Aber Sie sehen, wir kommen jetzt zu ziemlich konkreten Vorstellungen schon mit dieser Terminologie. Wir sagten: Etwas Wirkliches liegt zugrunde, wenn wir Formeln brauchen wie diese für w. Wir sprechen da von Wärmeäther; irgend etwas Wirkliches liegt zugrunde, wenn wir:diese Formeln (2) zu gebrauchen haben, bei denen das, was in den Formeln (1) positiv ist, negativ erscheinen muß, und sprechen dann von chemischem Äther; wir sprechen von Lichtäther, wenn wir nötig haben zum Imaginären zu schreiten in unseren Formeln; und wir sprechen tatsächlich von Lebensäther, wenn wir nötig haben mathematische Formeln zu gebrauchen, die wir noch gar nicht in Wirklichkeit haben, über die wir uns nicht klar sind, über die wir uns ebenso unklar sind in der Mathematik, wie die Naturforscher über das Leben sich unklar sind.
[15 ] Sie sehen hier einen sehr interessanten Parallelismus zwischen dem Gang des Denkens innerhalb der Mathematik und dem Gang des Denkens innerhalb der Naturwissenschaft selbst, woraus Sie ersehen können, daß es sich wirklich zunächst nicht um eine objektive Schwierigkeit handeln kann, sondern daß es sich handeln muß um eine subjektive Schwierigkeit. Denn ganz unabhängig von der Naturforschung tritt auf dem Gebiete der reinen Mathematik derselbe Gang des Denkens auf, und doch wird niemand glauben, daß er aus ebensolchen Erwägungen heraus einen schön stilisierten Vortrag halten könnte über die Grenzen des inneren mathematischen Erkennens wie Du Bois-Reymond über die Grenzen des Naturerkennens. Wenigstens mit derselben Art der Schlußfolgerung könnte man das nicht. Innerhalb des Mathematischen muß es möglich sein, wenn einem die Begriffe und Formulierungen nicht durch ihre Komplikation entschlüpfen, wenn man sie fassen will, im Gebiete des rein Mathematischen muß es möglich sein, zu abschließenden Formulierungen zu kommen. Die erwähnte Schwierigkeit kann nur etwas sein, was mit unseren relativen Unvollkommenheiten zusammenhängt, es kann dabei nicht gedacht werden, daß es sich um wirkliche Grenzen des menschlichen Erkennens handeln könnte. Es ist sehr wichtig, so etwas gründlich ins Auge zu fassen. Denn daran zeigt sich erstens, daß die einfache Anwendung der Mathematik nicht geht, solange wir im Physikalischen die Wirklichkeit ergreifen wollen. Denn wir können nicht einfach, wie es die Energetiker machen, sagen: Es verwandelt sich ein Wärmequantum in ein Quantum chemischer Energie und umgekehrt. Das dürfen wir nicht sagen, sondern dann, wenn so etwas geschieht, ergibt sich die Notwendigkeit, andere Zahlenwerte einzuführen. Dann ergibt sich die Notwendigkeit, wirklich die Hauptsache nicht darin zu sehen, daß mechanisch die eine Energieart die andere anregt, sondern daß man es zu tun hat mit einem wirklich qualitativen Umwandeln, was sich schon in der Zahl fassen läßt, wenn die eine Energie, wie man sagt, in die andere übergeht.
[ 16 ] Würde man aufmerksam geworden sein auf dieses selbst schon in den Zahlen festzuhaltende qualitative Umwandeln der einen Energieart in die andere, so würde man nicht zu der Vorstellung vorgerückt sein, die da sagt: Nun ja, so obenhin ist Wärme eben das, was wir als Wärme empfinden, ist mechanische Arbeit, was wir als solche empfinden, ist chemische Energie, was sich zeigt in chemischen Vorgängen; innerlich ist das alles gleich. Mechanische Bewegung vollzieht sich. Wärme ist auch nichts anderes. — Auf dieses Stoßen, Drängen der Moleküle oder Atome gegeneinander, an die Wände und so weiter, auf dieses Streben nach einer abstrakten Einheit für alle Energien, die eben eine mechanische Bewegung ist, würde man nicht gekommen sein, wenn man gesehen hätte, daß man, schon wenn man Rechnungsansätze macht, nötig hat, die Qualitätsunterschiede der Energien in Betracht zu ziehen. Es ist deshalb interessant, daß Eduard von Hartmann, als er die Wärmelehre philosophisch betrachtete, nötig hatte, Definitionen zu finden für die Physik, die von allem Qualitativen absehen. Dann natürlich kann man in der Physik nur eine eindeutige Mathematik finden. Und abgesehen von den Fällen, wo sich etwas aus den rein mathematischen Beziehungen als negativ ergibt, lieben es die Physiker nicht, mit solchen Zahlen-Qualitätsunterschieden in der Physik selbst zu rechnen. Sie rechnen mit positiv und negativ, aber das sind Dinge, die sich nur aus mathematischen Verhältnissen ergeben. Niemals würde man in der gewöhnlichen Energielehre gerechtfertigt finden, dadurch, daß eine Energie Wärme, eine andere chemische Energie ist, die eine mit positivem und die andere mit negativem Vorzeichen zu bezeichnen.
Twelfth Lecture
[ 1 ] Unfortunately, we have to postpone the experiments we had planned for today until tomorrow. They will be ready tomorrow to be shown as I need them to be if I want to discuss everything that is to be tested. We will therefore insert a consideration today of those things that we still need, then tomorrow we will set up the experiments so that we can bring the considerations to a preliminary conclusion the day after tomorrow.
[ 2 ] What I would like to mention first as an aid to our views, which we must develop with regard to the heat entity, is that I must point out to you that there is a certain difficulty in understanding what a transparent body actually is. I am not talking about heat now. But you will see, especially when we have completed these experiments, how we will gain an auxiliary concept of light for understanding the nature of heat. There is a certain difficulty, I say, in understanding what a relatively transparent body is and what an opaque body is, that is, a body that shows itself to us, so to speak, under the influence of light. I must speak somewhat differently than is usually done. The language of ordinary physics would say: An opaque body is one that, due to a certain quality of its surface, reflects the rays of light that fall on it and thus becomes visible as a body. I cannot choose these forms of expression because they are by no means a reproduction of the facts, but because they are expressions of already existing, specific theories that we cannot simply take for granted. For to speak of rays, to speak of rays of light, is theory. I have already spoken about this in my previous course. Everything we encounter in reality is not a ray of light, but an image, and that is something that must be noted. Furthermore, we cannot simply say: a transparent body is one that allows light to pass through it due to its internal molecular structure, and an opaque body is one that reflects light. For how could such a theory be justified without further ado? And if you remember what I have presented in recent days as the conditions of the realms of reality: solid, liquid, and gaseous bodies; thermal beings; \(x\), \(y\), \(z\), and then, adjacent to the solid bodies, the \(U\) realm, you will see that the realm of light must be related in some way to the realm of heat, and that the realm of chemical processes must also be related. On the other hand, what we encounter I would like to say, as the liquid form in the heat entity, in the air entity, be related in some way to what is the true essence of sound. For sounds appear on the occasion of compressions and rarefactions in gaseous or airy bodies.
[ 3 ] We can therefore initially assume that somewhere where we have assumed \(x\), \(y\), \(z\), the essence of light can also be found. But the question is whether, where we are looking for the essence of light, we also have to look for, for example, the essence of the transparency of certain bodies. This essence of the transparency of certain bodies cannot be sought directly from the essence of light or only from the relationships of light to solid bodies. We have the \(U\)-region, and this \(U\)-region must have some kind of relationship with solid bodies on the surface of the Earth. And we will at least have to raise the question and work toward answering it in these considerations that are still available to us in my presence: What influence does the \(U\)-region have on solid bodies, and can the difference that occurs between transparent bodies and the usually opaque metals reveal something of this influence to us? So these are the questions we must first address. And we will find the way to answer such questions if we now try to supplement what we learned yesterday about the nature of heat with a few other concepts.
[ 4 ] Within the field of physics, of course, we have seen the facts that arise as heat phenomena. We have seen facts such as those that we have thought of under the concept of heat conduction, which we have also demonstrated to you. Above all, we have observed this type of heat propagation in heat conduction, i.e., in the flow of heat either through a body or beyond the point of contact through two or more bodies in contact with each other. This flow of heat was imagined in one's mental image as if there were some kind of indefinite fluid, initially only as an image of the flow of heat, of the state of heat. And now we can already tie in with what external observation offers us: just as water somehow flows in a stream, that is, it is at a later point than before, which is what nature represents as flowing, so we can also follow the flow of heat from one point to another when so-called heat conduction takes place. A wide variety of people have thought about this flow of heat in the sense of heat conduction. Quite clear mental images—we could also start from others—come from Fourier, and we want to build on these a little and then see how we can reconcile these mental images with the insights we have already gained.

[ 5 ] With a mental image: we are faced with a closed body, some kind of metal, which would be sharply limited here by a plane, and here also by a plane. We can imagine it extending upwards and downwards into infinity. By keeping this boundary of the metal in boiling water, we try to maintain it at a temperature \(U_1\), which in this case could be around \(100°C\), and we try to keep the other boundary in contact with melting ice so that we have a temperature \(U_2\), which in this specific case could be \(0°C\). If you consider the whole situation, we are dealing with a difference: here \(U_1\), here \(U_2\); \(U_1-U_2\) gives us a temperature difference. The way heat conduction takes place will depend on this temperature difference. Because, of course, if the temperature difference is large, heat conduction must take place differently than if the temperature difference is smaller. I don't need a large amount of heat if this temperature difference is smaller, I need a larger amount of heat if this difference is larger in order to achieve the same effect, so I have to say: The amount of heat I need to achieve a certain effect will depend on this temperature difference \(U_1-U_2\);. It will also depend not only on this difference \(U_1-U_2\), but if I denote the length of the body by \(l\), the amount of heat I need to achieve a certain effect will be smaller when this length is large than when this length is small. That is, the amount of heat will be inversely proportional to \(l\). For a specific cross-section, which I will denote as \(q,\) I will be able to calculate the amount of heat I need to achieve a certain effect of heat conduction. The larger this cross-section is, the more heat I will need; the smaller the cross-section is, the less heat I will need. So \(q\) is directly proportional, and I will have to multiply by it. Then, finally, the whole thing will depend on time. I will have to multiply by time. Of course, since all these variables do not readily give me heat, I will then have to multiply the whole thing by something that already contains heat—because none of this is heat—by a constant that represents the measure of heat, by \(c\), and then I will get my amount of heat \(w\). This amount of heat \(w\) is therefore directly proportional to \(U_1-U_2\) and inversely proportional to the other factors. You see, if you compare all other factors with \(U_1\) and \(U_2\) in this context, you realize that what is actually flowing here is not directly a state of heat, or anything related to heat, but rather a heat gradient, a difference in level. I ask you to always keep this in mind. Just as one is dealing with a difference in level when, for example, water is allowed to fall from above into a sluice and sets a paddle wheel in motion, and just as the driving force that is developed there depends on the difference in level that must be taken into account, so here too one is dealing with a gradient, and that is what we must pay particular attention to.
[ 6 ] Now, if we want to get closer to the nature of heat, we must also consider another of Fourier's ideas, so that we can, in a sense, rectify these common mental images and proceed in our considerations in a manner more in line with reality than the physicists of the 19th and 20th centuries did. I have now essentially only considered what happens when heat is conducted from one end of the body to the other, but I assume that something else is going on inside the bodies themselves. I now ask: If, hypothetically, the heat did not simply progress evenly from left to right, but unevenly inside, how would I have to apply these formulas to the internal irregularities? So if there were irregularities in the distribution of heat, if the heat were conducted from here to here (compare the connecting line inside the metal) and so on, I would have to take this internal conduction of heat into account somehow. I would then have to consider the changes in these differences that are revealed inside, I would have to consider what happens in the body itself in terms of temperature compensation. As you can easily see, this would transform my formula. I would first have to say:
$$w = \frac{U_1-U_2}{l} \cdot t \cdot c \cdot q.$$
Now I am no longer dealing with the length \(l\) that is here, but with small distances. And I want to consider what happens on these small distances, just as it happens across the entire width here: the factor \(\frac{U_1-U_2}{l}.\) So, I am looking at this for small distances \(d \ x\) within it. When I do that, this finite quotient simply transforms into \(\frac{d \ u}{d \ x}\), where \(u\) is the small change in the heat state. And if I look at this for a certain small amount of time, I would still have to multiply by \(d \ t\) — I could also omit \(d \ t\) at first if I disregard time. So in this w we would have the expression for the heat quantum that would have to be expended at each point, from the thing itself, during internal work of heat, in order to follow any necessary temperature gradients in all directions and to compensate for temperature gradients. You must form the mental image that this formula here represents
$$w = c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (1)$$
would express such effects that occur due to the internal 'temperature gradients in the bodies.

[ 7 ] In connection with this, I would now ask you to consider what we already hinted at yesterday and what will become very clear to us tomorrow when we have the corresponding experimental setups. Nevertheless, I can already mention today that we must bear in mind how the conditions of heating, luminescence, and chemical action occur in the spectrum. I already pointed this out yesterday: When I have an ordinary earthly spectrum, I have the actual light effects in the middle, the heat effects on this side, and the chemical effects on this side. Now the following is the case: we have seen that if we want to design an image for this spectrum, we cannot make this image, which is supposed to record light effects, heat effects, and chemical effects, into a straight line. We have to go out to the left (from the plane forward) if we draw the line for light like this (horizontally) in order to find the corresponding symbol for heat. For the chemical effects, we have to go here (from the plane backward). It could also be the other way around, but let's stick with it for now.

[ 8 ] So, we have no way of staying within this plane if we want to symbolically encompass heat; we have no way of staying within the plane if we want to symbolically encompass the chemical effects. We have to step outside the plane. And in order to grasp this whole thing, let's make it clear to ourselves: How should we actually describe it when we express some quantum of heat that is effective inside a body through this formula? How should we describe it if we had a chemical quantum that was quantitatively related to it? We would not be able to cope if we did not somehow introduce a term that indicates that, while we have to go outside with the heat, we have to go inside with the chemical effects. We cannot cope if we do not take this into account. If we consider w here as a positive quantity — we could also take it as a negative quantity — then, if it is important to us, we must seek the corresponding distribution of chemical effects, and we have no choice but to designate the corresponding
$$w = - c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (2)$$
This corresponds to the chemical effects.
And this
$$w = + c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t$$
corresponds to the thermal effects.
[ 9] In fact, these considerations already show us that we cannot simply choose quantities if we want to create formulas and if we want to express in these formulas that we are dealing with a field of observation or a field of action where heat and chemical effects occur. Even in ordinary combustion, where we want to relate the chemical process to the thermal effect, if we work with formulas, we simply have to use everything that we use positively for the thermal effect negatively for the corresponding chemical effects.
[ 10 ] If you now continue your considerations and see that the heat bends outwards, so to speak, and the chemical effects bend inwards (see drawing on page 182), then only what is present in the light actually remains in the plane. But if you have now reserved the + for the heat and the — for the chemical effects, then you can no longer get by with any positive or negative values for the light effects. You must apply everything you can only guess at, everything that has not even been clarified today, the relationship between positive and negative numbers and imaginary numbers, to the light effects, and when dealing with light effects, you must say:
$$w = \sqrt{-1} \cdot c \cdot q \cdot \frac{d \ u}{d \ x} \cdot d \ t \qquad (3)$$
This means that you have to calculate with imaginary numbers, with mathematically imaginary number ratios, in order to really be able to find relationships between light, heat, and chemical effects that are in a common field of experimentation.
[ 11 ] But we said to ourselves: This spectral band that we actually form within the Earth is basically just the stretched spectral circle, and the complete spectrum would have the peach blossom up here. If you were to form the spectral band into a circle using powerful forces, you would get the union of what appears to go to infinity on the left and to infinity on the right. And this union, as you can imagine, cannot simply be achieved by means of a circle. For if you go through the heat, you simultaneously go out and go there (forward); and if you go through the chemical effects, you go to the other side (backward). So you are now in a position: firstly, to go there, seemingly into infinity, and secondly, to go there, seemingly into infinity. You not only have the unpleasant task of going there in a straight line (from left to right) and seeking out the infinitely distant point and coming back on the other side, when this infinitely distant point (on the right) is the same as the other (left) — at least you are on one plane. But now you stray, go here (left front) and go there (right back) and cannot come back unless you assume that infinity here and there leads you to the same point. But as you go there, you also walk away into infinity. So you walk in such a way that you not only walk into infinity on one side, but you also walk up here (see lower drawing, the arrow on the left, which spatially means “front”) into infinity and have to come back from two infinities (corresponding to the horizontal and the direction of the arrows). So you are walking a doubly complicated path. Then you would first find this peach blossom here, not by simply bending it together, but by also turning it at a right angle to one side and then the other.
[ 12 ] Imagine you were to treat the color band with an electromagnet; you would also have to rotate this electromagnet. But that leads you to say: what you would find there, you could not describe with all these characters. You would have to resort to what was pointed out yesterday in the discussion: the super-imaginary number.
[ 13 ] Now, you may remember that we pointed out here that these hyper-imaginary numbers are controversial, that they are difficult to deal with mathematically, that they cannot be written down unambiguously, so to speak. There are mathematicians who doubt that we have any right to speak of these super-imaginary numbers at all. Here, physics itself does not immediately lead to a proper formulation of super-imaginary numbers, but the demand for these super-imaginary numbers leads us to realize that such super-imaginary numbers are necessary if we want to express in formulaic terms what happens first in the field of chemistry, light, and heat, and what happens when we go beyond that and come back up. Anyone who has an organ for this will find something highly peculiar here. They will find something which I believe, if thought through properly, will be of great benefit in providing an appropriate explanation of physical phenomena. What I mean is that one encounters the same difficulties when one considers the inorganic in natural science and moves from the concepts one forms within the field of the inorganic to the attempt to understand life. It doesn't work with inorganic mental images. It doesn't work. This is evident, on the one hand, in the fact that there are thinkers who say: The earthly-organic must have emerged from the inorganic through a kind of spontaneous generation. But it is impossible to connect anything real with this view at first. Other thinkers, such as Preyer and others like him, derive everything inorganic from the organic, thereby coming closer to the truth. They conceive of the earth as originally a living body, and they conceive of what is inorganic today as a separation, something that has died out of the organic. But even these people cannot get beyond a conventional image. The same difficulties that one encounters when dealing with pure natural concepts arise within mathematics itself when one attempts to use well-considered formulas to move from what can be grasped in the realm of heat, in the realm of light, in the realm of chemistry, to what exists somewhere where the color spectrum would close in a natural way — we must assume that this color spectrum will close somewhere: it will probably not close in the earthly realm. We must point out how mathematics, through its own considerations, faces the problem of life. With what it has at its disposal today, it can conquer that which lies within light, warmth, and chemistry, but it cannot conquer that which we obviously find connected with it: the closure of the spectrum, which, however, cannot be expressed by such formulas as the other.
[ 14 ] First of all, we help ourselves by simply using terminology. But you see, we are already arriving at quite concrete mental images with this terminology. We said: something real underlies it when we need formulas like these for w. We are talking about heat ether; something real underlies it when we have to use these formulas (2), in which what is positive in formulas (1) must appear negative, and then we talk about chemical ether; we speak of light ether when we need to proceed to the imaginary in our formulas; and we actually speak of life ether when we need to use mathematical formulas that we do not yet have in reality, about which we are not clear, about which we are just as unclear in mathematics as natural scientists are unclear about life.
[ 15 ] Here you see a very interesting parallelism between the course of thought within mathematics and the course of thought within natural science itself, from which you can see that it really cannot be an objective difficulty at first, but that it must be a subjective difficulty. For quite independently of natural science, the same train of thought occurs in the field of pure mathematics, and yet no one would believe that, based on such considerations, one could give a beautifully stylized lecture on the limits of inner mathematical knowledge, as Du Bois-Reymond did on the limits of natural knowledge. At least, one could not do so with the same kind of conclusion. Within mathematics, it must be possible, if the concepts and formulations do not slip away due to their complexity when one wants to grasp them, to arrive at conclusive formulations in the field of pure mathematics. The difficulty mentioned can only be something related to our relative imperfections; it cannot be thought that it could be a matter of real limits of human cognition. It is very important to consider such a thing thoroughly. For it shows, first of all, that the simple application of mathematics does not work as long as we want to grasp reality in the physical realm. For we cannot simply say, as energy scientists do, that a quantum of heat is transformed into a quantum of chemical energy and vice versa. We cannot say that, but when something like this happens, it becomes necessary to introduce other numerical values. Then it becomes necessary to see that the main thing is not that one type of energy mechanically excites another, but that we are dealing with a truly qualitative transformation, which can already be captured in numbers when one energy, as they say, transitions into another.
[ 16 ] If one had become aware of this qualitative transformation of one type of energy into another, which can already be captured in numbers, one would not have advanced to the mental image that says: Well, at first glance, heat is what we perceive as heat, mechanical work is what we perceive as such, chemical energy is what manifests itself in chemical processes; internally, it is all the same. Mechanical motion takes place. Heat is nothing else. — This collision, this pushing and shoving of molecules or atoms against each other, against walls and so on, this striving for an abstract unity for all energies, which is precisely mechanical motion, would not have been conceived if it had been recognized that, even when making calculations, it is necessary to take into account the qualitative differences between energies. It is therefore interesting that Eduard von Hartmann, when he considered thermodynamics philosophically, needed to find definitions for physics that disregard everything qualitative. Then, of course, one can only find unambiguous mathematics in physics. And apart from cases where something turns out to be negative from purely mathematical relationships, physicists do not like to deal with such numerical differences in quality in physics itself. They deal with positive and negative, but these are things that arise only from mathematical relationships. In conventional energy theory, it would never be justified to designate one type of energy as heat and another as chemical energy, one with a positive sign and the other with a negative sign.

